��Ŀ����
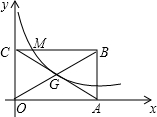
ֱ��l����A��1��0������˫����y=
(x��0)�ڵ�һ�����ڵ�B��2��1��������P��p+1��p-1����p��1����x���ƽ���߷ֱ���˫����y=
(x��0)��y=-
��x��0����M��N���㣬
��1����m��ֵ��ֱ��l�Ľ���ʽ��
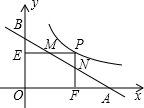
��2��ֱ��y=-x-3��x�ᡢy��ֱ��ڵ�C��D����E��ֱ��y=-x-3�ϣ��ҵ�E�ڵ������ޣ�ʹ��
=2��ƽ���߶�ED���߶�HQ����E��H��Ӧ����D��Q��Ӧ����ʹ��H��Qǡ�ö�����y=
��ͼ���ϣ���H��Q�������꣮
��3���Ƿ����ʵ��p��ʹ��S��AMN=4S��APM�������ڣ�����������������p��ֵ���������ڣ���˵�����ɣ�
| m |
| x |
| m |
| x |
| m |
| x |

��1����m��ֵ��ֱ��l�Ľ���ʽ��
��2��ֱ��y=-x-3��x�ᡢy��ֱ��ڵ�C��D����E��ֱ��y=-x-3�ϣ��ҵ�E�ڵ������ޣ�ʹ��
| CE |
| ED |
| m |
| x |
��3���Ƿ����ʵ��p��ʹ��S��AMN=4S��APM�������ڣ�����������������p��ֵ���������ڣ���˵�����ɣ�
��1���ɵ�B��2��1����y=
�ϣ���1=
����m=2��
��ֱ��l�Ľ���ʽΪy=kx+b��
�ɵ�A��1��0������B��2��1����y=kx+b�ϣ�
��
��
���
��
������ֱ��l�Ľ���ʽΪy=x-1��
��2����ֱ��y=-x-3��x�ᡢy��ֱ��ڵ�C��D����E��ֱ��y=-x-3�ϣ��ҵ�E�ڵ������ޣ�ʹ��
=2��
��D��ĺ������E��ĺ������1��D����������E���������С1��
��H��ĺ������Q��ĺ������1��H����������Q���������С1��
��H�������Ϊ��u��v����Q������꣨u+1��v-1������
��
���
��
������������ȥ����
��H�������Ϊ��1��2����Q������꣨2��1����
��3�����ڣ��������£�
��P������Ϊ��p+1��p-1����MN��x�ᣬ
���M��N�������궼Ϊp-1��
��M��
��p-1����N��-
��p-1�����ɵ�MN=
��
��S��AMN=
•
•��p-1��=2��
��p��1ʱ��S��APM=
��p+1-
����p-1��=
��p2-3����
��S��AMN=4S��APM��
��4��
��p2-3��=2��
���p1=-2���������⣬��ȥ����p2=2��
������������p��ֵΪ2��
| m |
| x |
| m |
| 2 |
��ֱ��l�Ľ���ʽΪy=kx+b��
�ɵ�A��1��0������B��2��1����y=kx+b�ϣ�
��
|
���
|
������ֱ��l�Ľ���ʽΪy=x-1��
��2����ֱ��y=-x-3��x�ᡢy��ֱ��ڵ�C��D����E��ֱ��y=-x-3�ϣ��ҵ�E�ڵ������ޣ�ʹ��
| CE |
| ED |
��D��ĺ������E��ĺ������1��D����������E���������С1��
��H��ĺ������Q��ĺ������1��H����������Q���������С1��
��H�������Ϊ��u��v����Q������꣨u+1��v-1������
|
���
|
|
��H�������Ϊ��1��2����Q������꣨2��1����
��3�����ڣ��������£�
��P������Ϊ��p+1��p-1����MN��x�ᣬ
���M��N�������궼Ϊp-1��
��M��
| 2 |
| p-1 |
| 2 |
| p-1 |
| 4 |
| p-1 |
��S��AMN=
| 1 |
| 2 |
| 4 |
| p-1 |
��p��1ʱ��S��APM=
| 1 |
| 2 |
| 2 |
| p-1 |
| 1 |
| 2 |
��S��AMN=4S��APM��
��4��
| 1 |
| 2 |
���p1=-2���������⣬��ȥ����p2=2��
������������p��ֵΪ2��

��ϰ��ϵ�д�
�����Ŀ



 �����Ƶ���ֲ�����60��70��ʾΪ���ڵ���60����С��70��������ͳ��ͼ��
�����Ƶ���ֲ�����60��70��ʾΪ���ڵ���60����С��70��������ͳ��ͼ��