Question

【题目】如图，在△ABC中，∠ACB=90°，点D为AB的中点，AC=3，cosA=，将△DAC沿着CD折叠后，点A落在点E处，则BE的长为（　　）

A. 5 B. 4 C. 7 D. 5

Answer 1

【答案】C

【解析】

连接AE，根据余弦的定义求出AB，根据勾股定理求出BC，根据直角三角形的性质求出CD，根据面积公式出去AE，根据翻转变换的性质求出AF，根据勾股定理、三角形中位线定理计算即可．

解：连接AE，

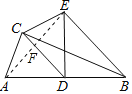
∵AC=3，cos∠CAB=，

∴AB=3AC=9，

由勾股定理得，BC==6，

∠ACB=90°，点D为AB的中点，

∴CD=AB=，

S△ABC=×3×6=9，

∵点D为AB的中点，

∴S△ACD=S△ABC=，

由翻转变换的性质可知，S四边形ACED=9，AE⊥CD，

则×CD×AE=9，

解得，AE=4，

∴AF=2，

由勾股定理得，DF==，

∵AF=FE，AD=DB，

∴BE=2DF=7，

故选：C．