Question

【题目】在中，，的平分线交于点，过点作交的平分线于点．

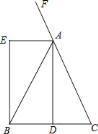
求证：四边形是矩形；

当满足什么条件时，四边形是正方形．

Answer 1

【答案】(1)见解析；（2）当时，四边形是正方形．理由见解析

【解析】

（1）先根据AB=AC，AD平分∠BAC，得∠BAD=12∠BAC，AD⊥BC，然后根据AE是△ABC的外角平分线，可求出AD⊥AE，然后根据有一个角是直角的平行四边形是矩形得到四边形ADBE为矩形；

（2）根据矩形的性质可知当∠BAC=90°时，则∠ABC=∠BAD=45°，利用等腰三角形的性质定理可知对应边AD=BD，再运用邻边相等的矩形是正方形，问题得证．

，

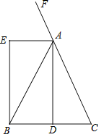
证明：∵，平分，

∴，，

∵是的外角平分线，

∴，

∵，

∴，即，

∴，

∵，

∴，

又∵，，

∴四边形是矩形；

解：当时，四边形是正方形．理由如下：

∵，平分，，

∴，

∴，

又∵四边形是矩形，

∴矩形为正方形．