题目内容
【题目】如图，在平面直角坐标系中，点
，点
，直线
交
轴于点
．
(1)求直线的表达式和点的坐标；
(2)在直线
上有一点
，使得
的面积为4，求点的坐标．
【答案】（1）
；
；（2）
【解析】
（1）首先设直线AB的解析式为
，然后将A、B两点坐标代入，即可得出解析式；当
时，即可得出点C的坐标；
（2）首先根据点A和O的坐标求出直线OA的解析式，然后分第一象限和第三象限设点P坐标，利用△BCP的面积构建方程即可得解.
（1）设直线AB的解析式为
将点
，点
代入解析式，得
解得
直线AB的解析式为
当时，
∴点C的坐标为
（2）∵
∴直线OA解析式为
当P在第一象限时,设点P的坐标为
,如图所示:
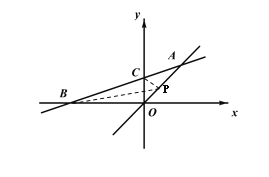
由题意，得
∵OB=4，OC=
∴
与在第一象限矛盾,故舍去;
当P在第三象限时,设点P的坐标为
,如图所示:
由题意,得
∴
∴
∴点P的坐标是.
练习册系列答案
相关题目
