题目内容
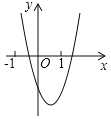
【题目】抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致是( )
在同一坐标系内的图象大致是( )
A.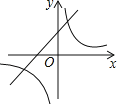 B.
B.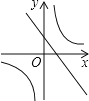
C.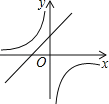 D.
D.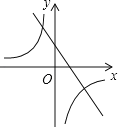
【答案】D
【解析】
根据二次函数开口方向,可以判断出a的正负,根据对称轴的位置和a的正负,可以判断出b的正负,再根抛物线与y轴的交点,可以判断出c的正负,然后根据a、b、c的正负去判断一次函数和二次函数在坐标系中的位置即可.
∵二次函数图象开口向上,
∴a>0,
∵对称轴为直线x=﹣![]() >0,
>0,
∴b<0,
当x=﹣1时,a﹣b+c>0,当x=1时,a﹣b+c<0,
∴(a+b+c)(a﹣b+c)<0,
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴一次函数图象经过第一、二、四象限,反比例函数图象经过第二四象限.
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
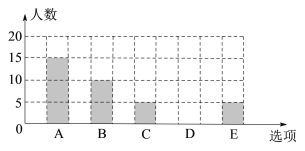
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.