Question

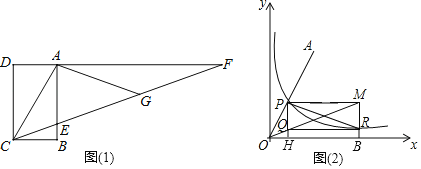
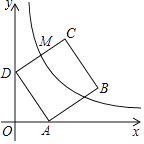
【题目】如图，正方形ABCD的顶点A、D分别在x轴、y轴上，∠ADO＝30°，OA＝2，反比例函y＝经过CD的中点M，那么k＝_____．

Answer 1

【答案】+6

【解析】

先根据△CDE≌△DAO，得到DE=AO=2，DO=2=CE，再根据F是CE的中点，即可得到F（，2+2），最后根据反比例函数y=的图象过CE的中点F，即可得到k的值．

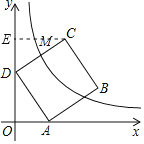
解：如图，作CE⊥y轴于点E．

∵正方形ABCD的顶点A、D分别在x轴、y轴上，

∴∠CED＝∠DOA＝90°，∠DCE＝∠ADO，CD＝DA，

∴△CDE≌△DAO（AAS），

∴DE＝AO＝2，

又∵∠ODA＝30°，

∴Rt△AOD中，AD＝2AO＝4，DO＝2＝CE，

∴EO＝2+2，

∴C（2，2+2），D（0，2），

∵M是CD的中点，

∴M（，1+2），

∵反比例函y＝经过CD的中点M，

∴k＝（1+2）＝+6，

故答案为：+6．