题目内容
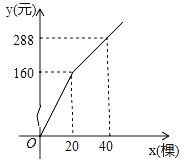
【题目】为了保护环境,某开发区综合治理指挥部决定购买A、B两种型号的污水处理设备共10台(注:要求同时有两种型号),买2台A型设备和3台B型设备共需要90万元,其中A型设备单价是B型设备单价的1.5倍;经预算,指挥部购买污水处理设备经费不超过180万元,请解答下列问题
(1)A型设备和B型设备的单价各是多少万元?
(2)指挥部有哪几种购买方案?
(3)若A型设备月处理污水量200吨、B型设各月处理污水量180吨,现要求月处理污水量不低于1840吨,设购买设备需要总费用为y万元,A型设备x台,请写出y与x的函数解析式,并根据函数性质选择更省钱的购买方案?
【答案】(1)A型设备和B型设备的单价各是22.5万元、15万元;(2)4种购买方案;(3)当购买A型设备2台,B型设备8台更省钱
【解析】
(1)根据题意,可以得到关于A、B单价的二元一次方程组,从而可以解答本题;
(2)根据题意可以得到相应的不等式,从而可以解答本题;
(3)根据题意可以得到y与x的函数关系式,然后利用一次函数的性质即可解答本题.
解:(1)设A型设备和B型设备的单价各是x万元、y万元,
![]() ,得
,得![]() ,
,
答:A型设备和B型设备的单价各是22.5万元、15万元;
(2)设购买A型设备a台,则购买B型设备(10﹣a)台,
22.5a+15(10﹣a)≤180,≤4
解得,a≤4,
∵a≥1,
∴1≤a≤4,
∴共有4种购买方案,
方案一:购买A型设备1台,B型设备9台;
方案二:购买A型设备2台,B型设备8台;
方案三:购买A型设备3台,B型设备7台;
方案四:购买A型设备4台,B型设备6台;
(3)由题意可得,
y与x的函数解析式是:y=22.5x+15(10﹣x)=7.5x+150,
即y与x的函数解析式是y=7.5x+150,
∵A型设备月处理污水量200吨、B型设各月处理污水量180吨,现要求月处理污水量不低于1840吨,
∴200x+180(10﹣x)≥1840,
解得,x≥2,
由(2)知x≤4,
∴2≤x≤4,
∴当x=2时,y取得最小值,此时y=165,
即当购买A型设备2台,B型设备8台更省钱.

 阅读快车系列答案
阅读快车系列答案【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.