��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��ax2��2x+c��ͼ����x�ύ��A��B���㣬��A��ԭ�����࣬��B������Ϊ��3��0������y�ύ�ڵ�C��0����3������P��ֱ��BC�·�����������һ���㣮
��1������κ����ı���ʽ��
��2������P�˶��������߶���ʱ�����ı���ABPC�������
��3����Q��x���ϵ�һ�����㣬����P���C���ڶԳ���Գ����Ե�B��C��P��QΪ������ı�����ƽ���ı���ʱ�����Q�����꣮
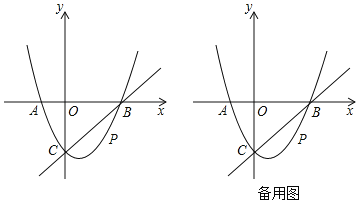
���𰸡���1��y��x2��2x��3����2��9����3��Q1��5��0����Q2��1��0����
��������
��1�����ô���ϵ������B��3��0����C��0��-3��������������y��ax2��2x+c���������ʽ���ɣ�
��2�����ı���ABPC�����������ָ�ΪS��AOC+S��OCP+S��OPB������������ε�������ɵó���
��3�����B��C��P��Q�������ٸ���ƽ���ı��ε����ʼ��ɽ��
�⣺��1����B��3��0����C��0����3��������������y��ax2��2x+c�ã�
![]() ��
��
���![]() ��
��
����κ����ı���ʽΪ��y��x2��2x��3��
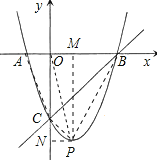
��2����ͼ������P�˶��������߶���ʱ������AC��PC��PB��PO����PM��AB��PN��OC��
�߶��κ����ı���ʽΪy��x2��2x��3��
��P�������Ϊ��1����4������PN��1��PM��4�����ɵó�OB��3��OC��3��AO��1��
���ı���ABPC�������S��AOC+S��OCP+S��OPB
��![]() ��
��
��![]() ��
��
��9��
��3���ߵ�P���C���ڶԳ���Գƣ���C��0����3����
��P��2����3����PC��2��
�ߵ�Q��x���ϣ����Q��x��0����
��B��3��0����
��BQ��|x��3|��
���Ե�B��C��P��QΪ������ı�����ƽ���ı���ʱ��
��BQ��PC����BQ��PC��
��|x��3|��2��
��ã�x1��5��x2��1��
��Q1��5��0����Q2��1��0����

 ��У����ϵ�д�
��У����ϵ�д�