Question

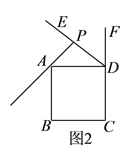
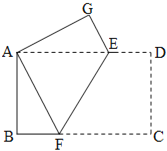
【题目】长方形具有四个内角均为直角，并且两组对边分别相等的特征.如图，把一张长方形纸片ABCD折叠，使点C与点A重合，折痕为EF.

（1）如果∠DEF＝123°，求∠BAF的度数；

（2）判断△ABF和△AGE是否全等吗？请说明理由.

Answer 1

【答案】（1）∠BAF的度数为24°；（2）△ABF≌△AGE，理由见解析.

【解析】试题分析：（1）由∠DEF的度数以及AD∥BC可求出∠EFC的度数，因为翻折，所以∠AFE =∠EFC，不难求出∠AFB的度数，即可求出∠BAF的度数；（2）△ABF≌△AGE，由已知条件不难证明AB=AG，∠BAF=∠GAE，∠B=∠G，故可证明△ABF≌△AGE.

试题解析：

（1）∵四边形ABCD是长方形，

∴AB＝CD，∠B＝∠DAB＝90°，AD∥BC.，

∴∠AEF＝∠CFE，

∵∠DEF+∠AEF＝180°，且∠DEF＝123°，

∴∠AEF＝57°，

∴∠CFE＝57°，

∵四边形CDEF与四边形AGEF关于EF对称，

∴四边形CDEF≌四边形AGEF，

∴∠G＝∠C＝∠D＝∠GAF＝90°，AG＝CD，∠AFE＝∠CFE，

∴∠AFE＝57°，

∵∠BFA+∠AFE+∠CFE＝180°，

∴∠BFA＝66°，

∵∠BFA+∠BAF＝90°，

∴∠BAF＝24°，

（2）△ABF≌△AGE，理由如下：

∵AG＝CD，

∴AB＝AG，

∵∠BAE＝90°，∠GAF＝90°，

∴∠BAE＝∠GAF，

∴∠BAE－∠EAF＝∠GAF－∠EAF，

∴∠BAF＝∠GAE，

在△ABF和△AGE中，

，

∴△ABF≌△AGE（ASA）.