题目内容
【题目】如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.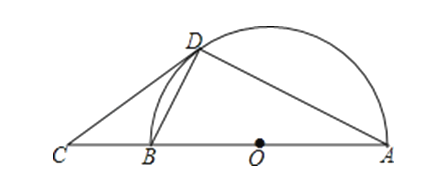
(1)求证:∠BAD=∠BDC;
(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)
【答案】
(1)
证明:(1)连接OD,如图,

∵CD与半圆O相切于点D,
∴OD⊥CD,
∴∠CDO=90°,即∠CDB+∠BDO=90°,
∵AB是半圆O的直径,
∴∠ADB=90°,即∠ADO+∠BDO=90°,
∴∠CDB=∠ODA,
∵OD=OA,
∴∠ODA=∠BAD,
∴∠BAD=∠BDC;
(2)
∵∠BAD=∠BDC=28°,在Rt△ABD中,sin∠BAD=![]() ,
,
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.
【解析】(1)连接OD,利用切线的性质和直径的性质转化为角的关系进行证明即可;
(2)根据三角函数进行计算即可.
【考点精析】通过灵活运用切线的性质定理和解直角三角形,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.

练习册系列答案
相关题目