题目内容
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.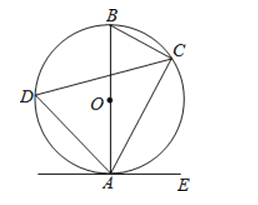
(1)求证:直线AE是⊙O的切线
(2)若∠D=60°,AB=6时,求劣弧![]() 的长(结果保留π)
的长(结果保留π)
【答案】
(1)
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CBA+∠CAB=90°,
∵∠EAC=∠B,
∴∠CAE+∠BAC=90°,
即 BA⊥AE.
∴AE是⊙O的切线.
(2)
解:连接CO,
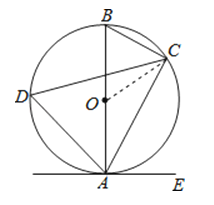
∵AB=6,
∴AO=3,
∵∠D=60°,
∴∠AOC=120°,
∴![]() =
=![]() =2π.
=2π.
【解析】(1)根据圆周角定理可得∠ACB=90°,进而可得∠CBA+∠CAB=90°,由∠EAC=∠B可得∠CAE+∠BAC=90°,从而可得直线AE是⊙O的切线;
(2)连接CO,计算出AO长,再利用圆周角定理可得∠AOC的度数,然后利用弧长公式可得答案.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目