题目内容
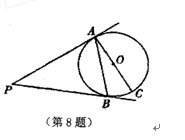
如图,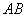 为半圆
为半圆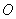 的直径,延长
的直径,延长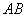 到点
到点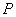 ,使
,使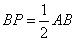 ,
,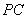 切半圆
切半圆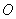 于点
于点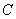 ,点
,点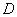 是弧AC上和点
是弧AC上和点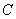 不重合的一点,则
不重合的一点,则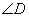 的度数为 .(圆的性质、切线的性质、解三角形)
的度数为 .(圆的性质、切线的性质、解三角形)
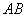 为半圆
为半圆 的直径,延长
的直径,延长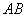 到点
到点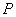 ,使
,使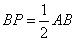 ,
,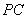 切半圆
切半圆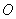 于点
于点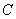 ,点
,点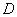 是弧AC上和点
是弧AC上和点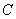 不重合的一点,则
不重合的一点,则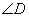 的度数为 .(圆的性质、切线的性质、解三角形)
的度数为 .(圆的性质、切线的性质、解三角形) 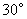
连接OC,由切线的性质得OC⊥PC,于是易得Rt△OCP中,OC=OB=PB;利用30°所对的边等于斜边的一半,可得∠P=30°,于是得∠COP=60°,再由“同弧所对的圆周角等于它所对的圆心角的一半”得∠CDB=30度.
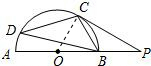 解:连接OC,
解:连接OC,
∵PC切半圆O于点C,
∴OC⊥PC,
∴OC=OB=PB,
∴∠P=30°,即∠COP=60°,
∴∠CDB=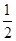 ∠COP=30°.
∠COP=30°.
 解:连接OC,
解:连接OC,∵PC切半圆O于点C,
∴OC⊥PC,
∴OC=OB=PB,
∴∠P=30°,即∠COP=60°,
∴∠CDB=
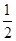 ∠COP=30°.
∠COP=30°.
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
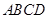 内接于
内接于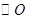 ,
,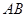 为
为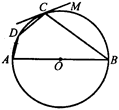
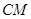 切
切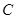 ,
, 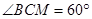 ,则
,则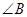 的正切值是( )
的正切值是( )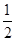
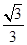
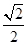
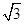
 ABC的两直角边AC、BC分别是一元二次方程
ABC的两直角边AC、BC分别是一元二次方程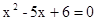 的两根,则此Rt
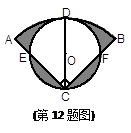
的两根,则此Rt 图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连
图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连 接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过. 为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
 ,
, ,则向量
,则向量 可表示为( ).
可表示为( ).



