题目内容
【题目】定义:在一个三角形中,若存在两条边x和y,使得y=x2,则称此三角形为“平方三角形”,x称为平方边.
(1)“若等边三角形为平方三角形,则面积为![]() 是 命题;“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题;(填“真”或“假”)
是 命题;“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题;(填“真”或“假”)
(2)若a,b,c是平方三角形的三条边,平方边a=2,若三角形中存在一个角为60°,求c的值;
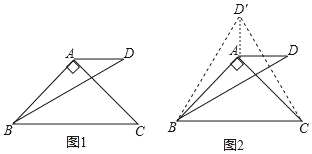
(3)如图,在△ABC中,D是BC上一点.
①若∠CAD=∠B,CD=1,求证,△ABC是平方三角形;
②若∠C=90°,BD=1,AC=m,CD=n,求tan∠DAB.(用含m,n的代数式表示)

【答案】(1)真,假;(2)c的长为4或1+![]() ;(3)①见解析;②tan∠DAB=
;(3)①见解析;②tan∠DAB=![]()
【解析】
(1)①根据平方三角形的定义,求出等边三角形的边长即可判断.②分两种情形分别判断即可.
(2)为a,b,c是平方三角形的三条边,平方边a=2,三角形中存在一个角为60°,只有∠B或∠C=60°,∠A不可能为60°,不妨设∠B=60°,BC=2,分两种情形:如图1中,①当c=a2时.②如图2中,当b=a2=4时,作CH⊥AB于H.求出AB即可.
(3)①证明△CAD∽△CBA,利用相似三角形的性质即可解决问题.
②如图4中,作DH⊥AB于H.利用相似三角形的性质求出DH,AH即可解决问题.
解:(1)∵等边三角形为平方三角形,
∴根据平方三角形的定义可知:等边三角形的边长为1,
∴等边三角形的面积=![]() ,
,
∴①是真命题.
当直角三角形中,30°所对的直角边为2时,斜边为4,满足平方三角形的定义,
当直角三角形中,和30°相邻的直角边是2时,不是平方三角形,
故②是假命题,
故答案为真,假.
(2)因为a,b,c是平方三角形的三条边,平方边a=2,三角形中存在一个角为60°,
只有∠B或∠C=60°,∠A不可能为60°,不妨设∠B=60°,BC=2,
如图1中,①当c=a2时,∵a=2,
∴c=22=4.
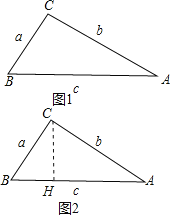
如图2中,当b=a2=4时,作CH⊥AB于H.
在Rt△BCH中,∵∠B=60°,∠CHB=90°,BC=2,
∴BH=![]() BC=1,CH=
BC=1,CH=![]() BH=
BH=![]() ,
,
在Rt△ACH中,AH=![]() =
=![]() ,
,
∴c=AB=BH+AH=1+![]() ,
,
综上所述,c的长为4或1+![]() .
.
(3)①如图3中,
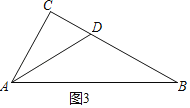
∵∠C=∠C,∠CAD=∠B,
∴△CAD∽△CBA,
∴![]() =
=![]() ,
,
∴AC2=CDCB,
∵CD=1,
∴AC2=BC,
∴△ABC是平方三角形.
②如图4中,作DH⊥AB于H.
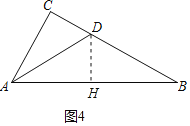
在Rt△ABC中,∵∠C=90°,AC=m,BC=CD+BD=1+n,
∴AB=![]() ,
,
∵DH⊥AB,
∴∠DHB=90°,
∵∠B=∠B,∠DHB=∠C=90°,
∴△BHD∽△BCA,
∴![]() ,
,
∴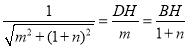 ,
,
∴DH=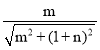 ,BH=
,BH=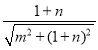 ,
,
∴AH=![]() ﹣
﹣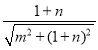 ,
,
∴tan∠DAB=![]() =
=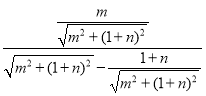 =
=![]() .
.

【题目】某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2010﹣2014这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
2010 | 2011 | 2012 | 2013 | 2014 |
234 | 233 | 245 | 247 | 256 |
(1)这五年的全年空气质量优良天数的中位数是________,平均数是________;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是________年(填写年份);
(3)求这五年的全年空气质量优良天数的方差________.