ЬтФПФкШн
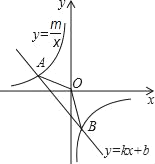
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓгыжБЯпyЃНxНЛгкЕуMЃЌЁЯAMBЃН90ЁуЃЌЦфСНБпЗжБ№гыСНзјБъжсЕФе§АыжсНЛгкЕуAЁЂBЃЌЫФБпаЮOAMBЕФУцЛ§ЮЊ6ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓгыжБЯпyЃНxНЛгкЕуMЃЌЁЯAMBЃН90ЁуЃЌЦфСНБпЗжБ№гыСНзјБъжсЕФе§АыжсНЛгкЕуAЁЂBЃЌЫФБпаЮOAMBЕФУцЛ§ЮЊ6ЃЎ
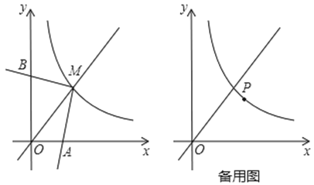
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉЕуPдкЃЈ1ЃЉЕФЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌШєЕуPЕФКсзјБъЮЊ3ЃЌдкxжсЩЯгавЛЕуDЃЈ4ЃЌ0ЃЉЃЌШєдкжБЯпyЃНxЩЯгаЖЏЕуCЃЌЙЙГЩЁїPDCЃЌЦфУцЛ§ЮЊ3ЃЌЧыаДГіCЕуЕФзјБъЃЛ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌШєЕуPЕФКсзјБъЮЊ3ЃЌдкxжсЩЯгавЛЕуDЃЈ4ЃЌ0ЃЉЃЌШєдкжБЯпyЃНxЩЯгаЖЏЕуCЃЌЙЙГЩЁїPDCЃЌЦфУцЛ§ЮЊ3ЃЌЧыаДГіCЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєЁЯEPFЃН90ЁуЃЌЦфСНБпЗжБ№ЮЊгыxжсе§АыжсЃЌжБЯпyЃНxНЛгкЕуEЁЂFЃЌЮЪЪЧЗёДцдкЕуEЃЌЪЙPEЃНPFЃПШєДцдкЃЌЧѓГіЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉkЃН6ЃЛЃЈ2ЃЉТњзуЬѕМўЕФЕуCзјБъЮЊ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉДцдкЃЌЃЈ4ЃЌ0ЃЉКЭЃЈ6ЃЌ0ЃЉ
ЃЛЃЈ3ЃЉДцдкЃЌЃЈ4ЃЌ0ЃЉКЭЃЈ6ЃЌ0ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуMзїMCЁЭxжсгкЕуCЃЌMDЁЭyжсгкЕуDЃЌИљОнAASжЄУїЁїAMCЁеЁїBMDЃЌФЧУДSЫФБпаЮOCMD=SЫФБпаЮOAMB=6ЃЌИљОнЗДБШР§КЏЪ§БШР§ЯЕЪ§kЕФМИКЮвтвхЕУГіk=6ЃЛ
ЃЈ2ЃЉШчЭМ1-1жаЃЌбгГЄDPНЛOCгкЕуEЃЌзїDHЁЭOCгкHЃЎРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНЧѓГіECЕФГЄМДПЩНтОіЮЪЬтЃЛ
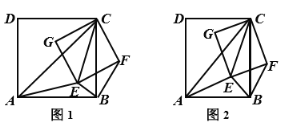
ЃЈ3ЃЉЯШИљОнЗДБШР§КЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЧѓЕУЕуPЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЎдйЗжСНжжЧщПіНјааЬжТлЃКЂйШчЭМ2ЃЌЙ§ЕуPзїPGЁЭxжсгкЕуGЃЌЙ§ЕуFзїFHЁЭPGгкЕуHЃЌНЛyжсгкЕуKЃЎИљОнAASжЄУїЁїPGEЁеЁїFHPЃЌНјЖјЧѓГіEЕузјБъЃЛЂкШчЭМ3ЃЌЭЌРэЧѓГіEЕузјБъЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуMзїMCЁЭxжсгкЕуCЃЌMDЁЭyжсгкЕуDЃЌ

дђЁЯMCAЃНЁЯMDBЃН90ЁуЃЌЁЯAMCЃНЁЯBMDЃЌMCЃНMDЃЌ
ЁрЁїAMCЁеЁїBMDЃЌ
ЁрSЫФБпаЮOCMDЃНSЫФБпаЮOAMBЃН6ЃЌ
ЁрkЃН6ЃЛ
ЃЈ2ЃЉШчЭМ1Љ1жаЃЌбгГЄDPНЛOCгкЕуEЃЌзїDHЁЭOCгкHЃЌзїPJЁЭOCгкJЃЌ

ЁпDЃЈ4ЃЌ0ЃЉЃЌPЃЈ3ЃЌ2ЃЉЃЌ
ЁржБЯпPDЕФНтЮіЪНЮЊyЃНЉ2x+8ЃЌ
гЩ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁрEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
дкRtЁїODHжаЃЌЁпЁЯDOHЃН45ЁуЃЌODЃН4ЃЌ
ЁрDHЃН2![]() ЃЌЭЌЗЈПЩЕУPJЃН
ЃЌЭЌЗЈПЩЕУPJЃН![]()
Ёп![]() ECDHЉ
ECDHЉ![]() ECPJЃН3ЃЌ
ECPJЃН3ЃЌ
ЁрECЃН2![]() ЃЌ
ЃЌ
ЁрТњзуЬѕМўЕФЕуCзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉДцдкЕуEЃЌЪЙЕУPEЃНPFЃЎ
гЩЬтвтЃЌЕУЕуPЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЎ
ЂйШчЭМ2ЃЌЙ§ЕуPзїPGЁЭxжсгкЕуGЃЌЙ§ЕуFзїFHЁЭPGгкЕуHЃЌНЛyжсгкЕуKЃЎ
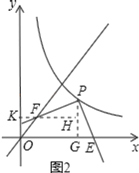
ЁпЁЯPGEЃНЁЯFHPЃН90ЁуЃЌЁЯEPGЃНЁЯPFHЃЌPEЃНPFЃЌ
ЁрЁїPGEЁеЁїFHPЃЌ
ЁрPGЃНFHЃН2ЃЌFKЃНOKЃН3Љ2ЃН1ЃЌGEЃНHPЃН2Љ1ЃН1ЃЌ
ЁрOEЃНOG+GEЃН3+1ЃН4ЃЌ
ЁрEЃЈ4ЃЌ0ЃЉЃЛ
ЂкШчЭМ3ЃЌЙ§ЕуPзїPGЁЭxжсгкЕуGЃЌЙ§ЕуFзїFHЁЭPGгкЕуHЃЌНЛyжсгкЕуKЃЎ

ЁпЁЯPGEЃНЁЯFHPЃН90ЁуЃЌЁЯEPGЃНЁЯPFHЃЌPEЃНPFЃЌ
ЁрЁїPGEЁеЁїFHPЃЌ
ЁрPGЃНFHЃН2ЃЌFKЃНOKЃН3+2ЃН5ЃЌGEЃНHPЃН5Љ2ЃН3ЃЌ
ЁрOEЃНOG+GEЃН3+3ЃН6ЃЌ
ЁрEЃЈ6ЃЌ0ЃЉЃЌ
ЙЪД№АИЮЊЃЈ4ЃЌ0ЃЉКЭЃЈ6ЃЌ0ЃЉЃЎ