��Ŀ����
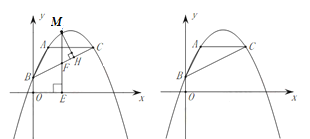
����Ŀ����ͼ����֪�ھ���ABCD�У�AB=4��BC=2����O��AB���ӳ����ϣ�OB=![]() ����AOE=60�㣬����P�ӵ�O��������ÿ��2����λ���ȵ��ٶ�������OE�����˶�����PΪԲ�ģ�OPΪ�뾶����P��ͬʱ��Q��B���������ÿ��1����λ���ȵ��ٶ�������B-C-D���D�˶���Q��D�غ�ʱ��P��Qͬʱֹͣ�˶�����P���˶�ʱ��t�룮
����AOE=60�㣬����P�ӵ�O��������ÿ��2����λ���ȵ��ٶ�������OE�����˶�����PΪԲ�ģ�OPΪ�뾶����P��ͬʱ��Q��B���������ÿ��1����λ���ȵ��ٶ�������B-C-D���D�˶���Q��D�غ�ʱ��P��Qͬʱֹͣ�˶�����P���˶�ʱ��t�룮
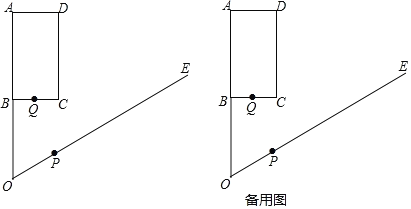
��1����BOC= ��PA����Сֵ�� ��
��2������P����Cʱ�����P���ӻ����߶�OAΧ�ɵķ��ͼ�ε������
��3������P�����ABCD�ı�����ֱ������ʱ����t��ֵ��
���𰸡���1��30����3+2![]() ����2��
����2��![]() ����3������tֵ����0��t��6��Χ֮�ڣ�����P�����ABCD�ı�����ֱ������ʱ��t��ֵ��
����3������tֵ����0��t��6��Χ֮�ڣ�����P�����ABCD�ı�����ֱ������ʱ��t��ֵ��![]() ��
��![]() ��4-2
��4-2![]()
��������
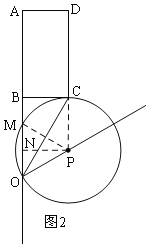
��1����ֱ�ǡ�OBC�У��ȸ�����ǵ��������BOC�Ķ��������ݴ��߶���̿�֪����AP��OPʱ��PA��ֵ��С���������Ǻ�����AP����Сֵ��
��2����ͼ2���������ߣ���������PCBN��ȷ����P���ӻ����߶�OAΧ�ɵķ��ͼ����С����OM���������������ȥ����������ɵý��ۣ�
��3�������������
�ٵ���P�����ABCD�ı�BC����ʱ���ǣ�2�����е��������ʱt![]() ��
��
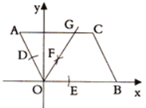
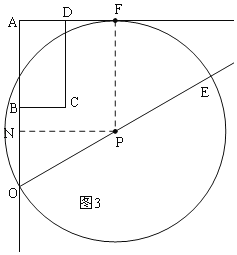
�ڵ���P�����ABCD�ı�AD����ʱ����ͼ3������AN+NO=AO��ʽ�ɵ�t��ֵ��
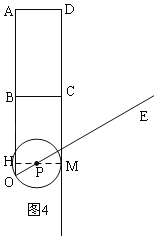
�۵���P�����ABCD�ı�CD����ʱ����ͼ4������PM+PH=BC��ʽ�ɵ�t��ֵ��
��1����ͼ1��
���ı���ABCD�Ǿ��Σ����ABC=90�㣬���OBC=90�㣬tan��BOC![]() �����BOC=30�㣮
�����BOC=30�㣮
��AP��OPʱ��PA��ֵ��С��
��OA=AB+OB=4+2![]() ����Rt��AOP�У��ߡ�AOE=60�㣬��sin60
����Rt��AOP�У��ߡ�AOE=60�㣬��sin60![]() ����AP
����AP![]() 3+2
3+2![]() ����PA����Сֵ��3+2
����PA����Сֵ��3+2![]() ��
��
�ʴ�Ϊ��30�㣬3+2![]() ��
��
��2����ͼ2��������ã�OP=�뾶r=2t������PC��PM����PC=PM=PO=r=2t�����POC=��PCO=��BOP����BOC=60�㩁30��=30�㣮
�ߡ�BCO=90�㩁��BOC=90�㩁30��=60�㣬���PCB=��BCO+��PCO=60��+30��=90�㣬���뾶PC��BC����ʱֱ��BC���P���У���
��PN��OM��N�����PNB=��NBC=��BCP=90�㣬���ı���PCBN�Ǿ��Σ���BN=PC=2t��
�ߡ�NOP=60�㣬����Rt��PNO�У���OPN=30�㣬��ON![]() OP=t��
OP=t��
��BN+ON=BO����2t+t=2![]() ����t
����t![]() ��r
��r![]() ���൱t
���൱t![]() ʱ����P������C��SС����OM=S����POM��S��POM��
ʱ����P������C��SС����OM=S����POM��S��POM��
�ߡ�POM=60����PO=PM�����POM�ǵȱ������Σ���OM=2ON=2t![]() ��PN
��PN![]() t=2����S����OM
t=2����S����OM![]() 2
2![]() ��
��![]() ��
��
�𣺡�P���ӻ����߶�OAΧ�ɵķ��ͼ�ε����Ϊ![]() ��
��![]() ��
��
��3���ٵ���P�����ABCD�ı�BC����ʱ���ǣ�2�����С�P����C����ʱt![]() ��
��
�ڵ���P�����ABCD�ı�AD����ʱ����ͼ3����P��PF��AD��F����P��PN��AO��N��AN=FP=r=2t��ON![]() OP=t��
OP=t��
��AN+NO=AO����2t+t=2![]() 4��t
4��t![]() ��
��
�۵���P�����ABCD�ı�CD����ʱ����ͼ4����PM��DC��M����OA��H����PM=OP=2t��PH![]() t��
t��
��PM+PH=BC����2t![]() t=2��t=4��2
t=2��t=4��2![]() ��
��
��������������P�����ABCD�ı�����ֱ������ʱt��ֵ��![]() ��
��![]() ��4��2
��4��2![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij�������꼶ѧ���μ�ѧҵˮƽ������⡣�����ȡ����25��ѧ���ijɼ�������Ϊ100�֣���ͳ�����£�
90��74��88��65��98��75��81��42��85��70��55��80��95��88��72��88��60��56��76��66��78��72��82��63��100.
��1��90�ּ�����Ϊ![]() ����75��89��Ϊ
����75��89��Ϊ![]() ����60��74��Ϊ
����60��74��Ϊ![]() ����60������Ϊ
����60������Ϊ![]() ��������������������
��������������������
�ȼ� |
|
|
|
|
���� |
|
| 8 |
|
��2�����ݣ�1������ɵı���֪�������ݵļ�����____����λ����____��������____.
��3���õ���ijѧУ���꼶����1000��ѧ�������60�ּ�����Ϊ��������Ƹ�У���꼶�μӴ˴�ѧҵˮƽ��������ж����˼���
��4����Ҫ֪�������ÿһ���ȼ�������ռ�������İٷֱȣ�Ӧѡ��_____ͳ��ͼ.