题目内容
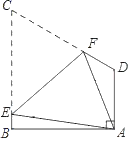
【题目】如图，在四边形ABCD中，∠A＝∠B＝90°，∠C＝60°，BC＝CD＝8，将四边形ABCD折叠，使点C与点A重合，折痕为EF，则BE的长为（ ）
A. 1B. 2C. 
D. 
【答案】A
【解析】
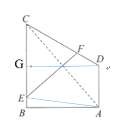
作DG⊥BC，连接AE，先根据Rt△CDG，∠DCG=60°，得出CG=4，利用勾股定理求出DG=4
，则AB= DG=4，设BE=x，则CE=8-x，根据折叠得AE= CE=8-x，再根据勾股定理在Rt△ABE列出方程进行求解.
作DG⊥BC，连接AE，
在Rt△CDG，∠DCG=60°，得出CG=4，
∴DG=4，则AB= DG=4，
设BE=x，则CE=8-x，根据折叠得AE= CE=8-x，
在Rt△ABE中，AE2=AB2+BE2，即(8-x)2=(4)2+x2
解得x=1，
故选A.
练习册系列答案
相关题目
