题目内容
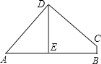
【题目】已知:正方形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,

![]() 四边形
四边形![]() 是正方形吗?为什么?
是正方形吗?为什么?
![]() 若正方形
若正方形![]() 的边长为
的边长为![]() ,且
,且![]() ,请求出四边形
,请求出四边形![]() 的面积.
的面积.
【答案】![]() 四边形
四边形![]() 是正方形;证明见解析;(2)10.
是正方形;证明见解析;(2)10.
【解析】
(1)根据正方形的性质证明AE=BF=CG=DH、∠A=∠B=∠C=∠D、AH=BE=CF=DG,利用SAS判定△AEH△BFE△CGF△DHG,即可得![]() ,所以四边形EFGH是菱形,再证明∠HEF=90°,即可判定四边形EFGH是正方形;(2)根据已知条件求得AE=BF=CG=DH=3,再由正方形
,所以四边形EFGH是菱形,再证明∠HEF=90°,即可判定四边形EFGH是正方形;(2)根据已知条件求得AE=BF=CG=DH=3,再由正方形![]() 的面积
的面积![]() 即可求得四边形
即可求得四边形![]() 的面积.
的面积.
![]() 四边形
四边形![]() 是正方形;
是正方形;
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 、
、![]() 、
、![]() 和
和![]() 中,
中,
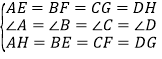 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∵![]() ,
,
∴![]() ,
,
∴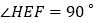 ,
,
∴四边形![]() 是正方形;
是正方形;
![]() ∵正方形
∵正方形![]() 的边长为
的边长为![]() ,且
,且![]() ,
,
∴![]() ,
,
∴正方形![]() 的面积
的面积![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目