题目内容
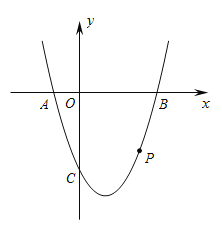
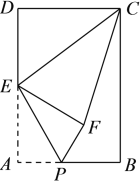
【题目】如图,△ABC与△CDE为等腰直角三角形,∠BAC=∠DEC=90°,连接AD,取AD中点P,连接BP,并延长到点M,使BP=PM,连接AM、EM、AE,将△CDE绕点C顺时针旋转.
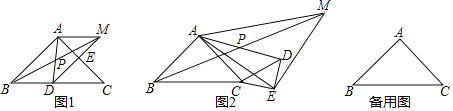
(1)如图①,当点D在BC上,E在AC上时,AE与AM的数量关系是______,∠MAE=______;
(2)将△CDE绕点C顺时针旋转到如图②所示的位置,(1)中的结论是否仍然成立,若成立,请给出证明,若不成立,请说明理由;
(3)若CD=![]() BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=
BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=![]() CD时,请直接写出α的值.
CD时,请直接写出α的值.
【答案】(1)AM=![]() AE , 45°;(2)成立,见解析;(3)α的值为60°或300°.
AE , 45°;(2)成立,见解析;(3)α的值为60°或300°.
【解析】
(1)证明四边形ABDM是平行四边形即可解决问题.
(2)如图2中,连接BD,DM,BD交AC于点O,交AE于G.证明△BCD∽△ACE,推出∠CBD=∠CAE,![]() =
=![]() ,即可解决问题.
,即可解决问题.
(3)如图2中,首先证明△AEM是等腰直角三角形,分两种情形画出图形分别求解即可.
解:(1)结论:AM=![]() AE,∠MAE=45°.
AE,∠MAE=45°.
理由:如图1中,
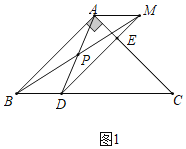
∵AP=PD,BP=PM,
∴四边形ABDM是平行四边形,
∴AM∥BC,
∴∠MAE=∠C,
∵AB=AC,∠BAC=90°,
∴∠C=45°,
∴∠MAE=45°,
∵∠AEM=∠DEC=90°,
∴∠AME=∠EAM=45°,
∴MA=![]() AE.
AE.
故答案为:AM=![]() AE,45°.
AE,45°.
(2)如图2中,连接BD,DM,BD交AC于点O,交AE于G.
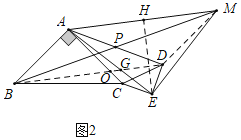
∵BC=![]() AC,CD=
AC,CD=![]() CE,
CE,
∴![]() =
=![]() ,
,
∵∠ACB=∠DCE=45°,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CBD=∠CAE,![]() =
=![]() ,
,
∴BD=![]() AE,
AE,
∵∠BOC=∠AOG,
∴∠AGO=∠BCO=45°,
∵AP=PD,BP=PM,
∴四边形ABDM是平行四边形,
∴AM∥BD,AM=BD=![]() AE,
AE,
∴∠MAE=∠BGA=45°,
∵EH⊥AM,
∴△AHE是等腰直角三角形,
∴AH=![]() AE,∵AM=
AE,∵AM=![]() AE,
AE,
∴AH=MH,
∴EA=EM,
∴∠EAM=∠EMA=45°,
∴∠AEM=90°.
(3)如图2中,作EH⊥AM于H.
∵EH⊥AM,∠MAE=45°,
∴△AHE是等腰直角三角形,
∴AH=![]() AE,∵AM=
AE,∵AM=![]() AE,
AE,
∴AH=MH,
∴EA=EM,
∴∠EAM=∠EMA=45°,
∴∠AEM=90°.
如图3-1中,
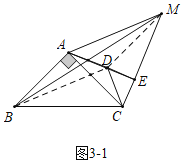
∵EM=EA=![]() CD,设CD=
CD,设CD=![]() a,则CE=a,BC=2
a,则CE=a,BC=2![]() a,AC=2a,EA=
a,AC=2a,EA=![]() a,
a,
∴AC2=AE2+EC2,
∴∠AEC=90°,
∴tan∠ACE=![]() =
=![]() ,
,
∴∠ACE=60°,
∴旋转角α=60°.
如图3-2中,同法可证∠AEC=90°,∠ACE=60°,此时旋转角α=300°.
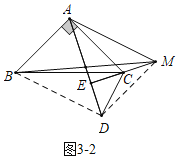
综上所述,满足条件的α的值为60°或300°.

 阅读快车系列答案
阅读快车系列答案【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.