题目内容
【题目】某酒店试销售某种套餐,试销一段时间后发现,每份套餐的成本为7元,该店每天固定支出费用为200元(不含套餐成本). 若每份售价不超过10元,每天可销售300份;若每份售价超过10元,每提高1元,每天的销售量就减少30份. 设该店每份套餐的售价为x(x≥7)元,每天的销售量为y份,每天的利润为M元.
(1)直接写出y与x的函数关系式;
(2)求出M与x的函数关系式;
(3)若该店既要吸引顾客,使每天的销售量较大,又要获取最大的利润,则每份套餐的售价应定为多少元(为了便于计算,每份套餐的售价取整数)?此时,最大利润为多少元?
【答案】(1)y=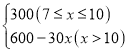 ;(2)M=
;(2)M= ;(3)当x=13时,M最大为1060
;(3)当x=13时,M最大为1060
【解析】
(1)先根据x的取值范围分类讨论,再根据题意即可求出y与x的函数关系式;
(2)先根据x的取值范围分类讨论,再根据“总利润=每份的利润×份数-每天固定支出费用”即可求出M与x的函数关系式;
(3)由(2)的关系式和一次函数、二次函数最值的求法即可得出结论.
解:(1)由题意可得:若每份售价不超过10元,每天可销售y=300份
若每份售价超过10元,y=300-30(x-10)=600-30x;
综上:y=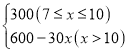
(2)由题意可得:当![]() 时,M=300(x-7)-200=300x-2300;
时,M=300(x-7)-200=300x-2300;
当![]() 时,M=(x-7)y-200
时,M=(x-7)y-200
=(x-7)(600-30x)-200
=-30x2+810x-4400
综上:M=
(3)当![]() 时,
时,
∵300>0
∴M随x的增大而增大
∴此时当x=10时,M最大,最大值为300×10-2300=700;
当x>10时,M=![]() =
=![]() ,其图象的开口向下,对称轴为直线x=
,其图象的开口向下,对称轴为直线x=![]()
∵x为整数
∴当x=13或14时,M最大,最大值为1060
∵使每天的销售量较大,
∴当x=13时,y=600-30×13=210;
当x=14时,y=600-30×14=180
故当x=13时,每天的销售量较大
∵700元<1060元
∴该店既要吸引顾客,使每天的销售量较大,又要获取最大的利润,则每份套餐的售价应定为13元,此时,最大利润为1060元.
答:该店既要吸引顾客,使每天的销售量较大,又要获取最大的利润,则每份套餐的售价应定为13元,此时,最大利润为1060元.

 备战中考寒假系列答案
备战中考寒假系列答案