题目内容
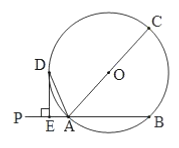
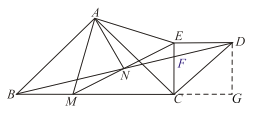
【题目】已知,如图,![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,![]() 于点
于点![]() 取
取![]() 的中点
的中点![]() 连接
连接![]() 并延长交
并延长交![]() 于
于![]() .连接
.连接![]() .
.

![]() ①直接写出:
①直接写出:![]() 与
与![]() 的位置关系是________,
的位置关系是________,![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
②请任意选择上述关系中的一个加以证明.
![]() 已知,
已知,![]() ,
,![]() 若
若![]() 与
与![]() 交于点
交于点![]() 求
求![]() 的长.
的长.
【答案】(1)①![]() ;②见解析;(2)
;②见解析;(2)![]() .
.
【解析】
(1)①根据![]() 和
和![]() 是等腰直角三角形,得到∠ABC=∠ACB=45°,根据
是等腰直角三角形,得到∠ABC=∠ACB=45°,根据![]() ,得到∠ECB=∠CED=90°,推出ED∥BC,证得∠EDN=∠MBN,从而证明△BMN≌△DEN,得到BM=EC,再证明△ABM≌△ACE,推出△MAE是等腰直角三角形,得到
,得到∠ECB=∠CED=90°,推出ED∥BC,证得∠EDN=∠MBN,从而证明△BMN≌△DEN,得到BM=EC,再证明△ABM≌△ACE,推出△MAE是等腰直角三角形,得到![]() ;
;
②如①的证明过程;
![]() 过点
过点![]() 作
作![]() 于点
于点![]() 得到四边形
得到四边形![]() 是正方形,由勾股定理求出
是正方形,由勾股定理求出![]() ,
,![]() ,得到
,得到![]() ,由勾股定理求出
,由勾股定理求出![]() ,根据
,根据![]() 证得△DEF∽△BCF,求出DF的长度.
证得△DEF∽△BCF,求出DF的长度.
(1)①∵![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
∴AB=AC,EC=ED,∠BAC=∠CED=90°,
∴∠ABC=∠ACB=45°,
∵![]() ,
,
∴∠ECB=∠CED=90°,
∴ED∥BC,
∴∠EDN=∠MBN,
∵N是BD的中点,
∴BN=DN,
∵∠BNM=∠END,
∴△BMN≌△DEN,
∴BM=DE,MN=EN,
∴BM=EC,
∵∠ECB=90°,∠ACB=45°,
∴∠ACE=∠ABC=45°,
∵AB=AC,
∴△ABM≌△ACE,
∴AM=AE,∠BAM=∠CAE,
∵∠BAM+∠CAM=90°,
∴∠MAE=∠CAE+∠CAM=90°,
∴△MAE是等腰直角三角形,
∵MN=NE,
∴![]() ,
,
故答案为:![]() ;
;
![]() 选
选![]() 给予证明:
给予证明:
![]() ,
,
![]()
![]()
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]()
在![]() 和
和![]() 中,
中,
![]() ,
,![]()
![]() ,
,
![]() ;
;
∵△ABC和![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
![]()
![]()
在![]() 和
和![]() 中,
中,
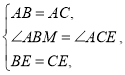
![]()
![]() ,
,![]() ,
,
![]()
即![]() ;
;
又![]() .
.
![]() ,
,
(说明:由![]() 可得
可得![]() );
);
![]() 过点
过点![]() 作
作![]() 于点
于点![]()
则四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
在等腰直角![]() 中,
中,
![]()
![]()
![]() ,
,
在直角![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
由![]() 得
得![]()
![]() ,
,
![]() ,
,
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
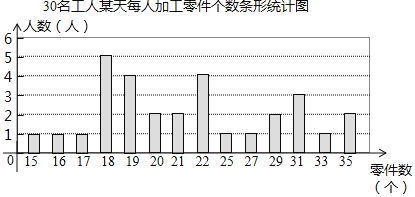
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.