题目内容
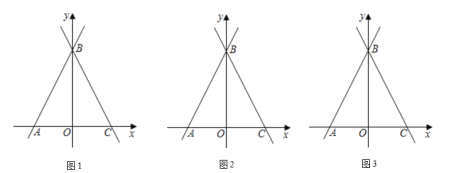
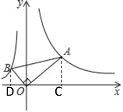
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点 A 在反比例函数![]() (x>0)的图象上,则经过点 B 的反比例函数解式为_________.
(x>0)的图象上,则经过点 B 的反比例函数解式为_________.

【答案】![]()
【解析】
过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,设A点坐标为(a,![]() ),根据锐角三角函数可得
),根据锐角三角函数可得![]() ,然后利用相似三角形的判定可证△DBO∽△COA,列出比例式可用a表示点B的坐标,利用待定系数法即可求出结论.
,然后利用相似三角形的判定可证△DBO∽△COA,列出比例式可用a表示点B的坐标,利用待定系数法即可求出结论.
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D
设A点坐标为(a,![]() )其中a>0
)其中a>0
∴OC=a,AC=![]()
∵在Rt△AOB中,∠OAB=30°,
∴tan∠OAB=![]()
∵∠BDO=∠OCA=∠AOB=90°
∴∠DBO+∠BOD=90°,∠COA+∠BOD=90°
∴∠DBO=∠COA
∴△DBO∽△COA
∴![]()
即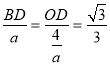
解得:BD=![]() ,OD=
,OD=![]()
∴点B的坐标为(![]() ,
,![]() )
)
设经过点 B 的反比例函数解式为![]()
将点B的坐标代入,得
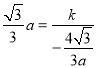
解得:k=![]()
∴经过点 B 的反比例函数解式为![]() .
.
故答案为:![]() .
.

【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
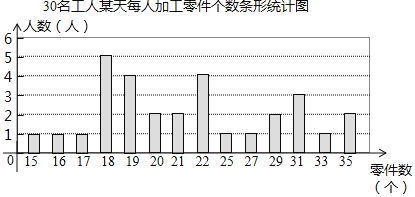
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.