题目内容
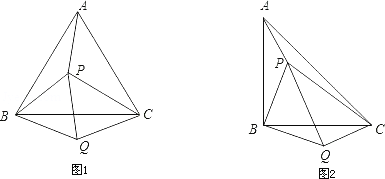
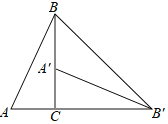
【题目】如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA，CB分别相交于点P，Q，则线段PQ的最小值（ ）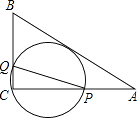
A.5
B.4 
C.4.75
D.4.8
【答案】D
【解析】解：线段PQ长度的最小值时，PQ为圆的直径，
如图，设QP的中点为F，圆F与AB的切点为D，连接FD、CF、CD，
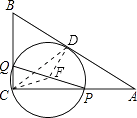
∵圆F与AB相切，∴FD⊥AB，
∵AB=5，AC=4，BC=3，
∴∠ACB=90°，FC+FD=PQ，
∴CF+FD＞CD，且PQ为圆F的直径，
∵当点F在直角三角形ABC的斜边AB的高上CD时，PQ=CD有最小值，即CD为圆F的直径，
且S△ABC= 
BCCA= CDAB，
∴CD= 
=4.8，即PQ的最小值为4.8，
所以答案是：D．
【考点精析】本题主要考查了三角形的面积和勾股定理的逆定理的相关知识点，需要掌握三角形的面积=1/2×底×高；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能正确解答此题．
练习册系列答案
相关题目
【题目】如图是连续十周测试甲、乙两名运动员体能情况的折线统计图，教练组规定：体能测试成绩70分以上(包括70分)为合适.
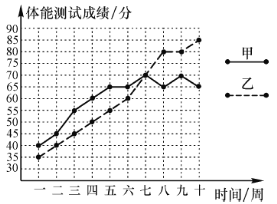
(1)请根据图中所提供的信息填写下表：
平均数 | 中位数 | 体能测试成绩合格次数（次） | |
甲 | 65 | ||
乙 | 60 |
(2)请从下面两个不同的角度对运动员体能测试结果进行判断：①依据平均数与成绩合格的次数比较甲和乙，哪个的体能测试成绩较好；②依据平均数与中位数比较甲和乙，哪个的体能测试成绩较好；
(3)依据折线统计图和成绩合格的次数，分析哪位运动员体能训练的效果较好.
