题目内容
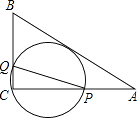
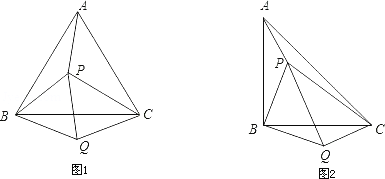
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
【答案】(1)证明见解析(2)满足:![]()
【解析】
由旋转得△BAP≌△BCQ 满足:![]()
∴PA=CQ PB=BQ 由旋转得△BAP≌△BCQ
∵∠PBQ=60![]() ∴PA=CQ PB=BQ
∴PA=CQ PB=BQ
∴△PBQ为等边三角形 ∠PBQ=![]()
∴PB=PQ ∴![]()
∵PA![]() +PB
+PB![]() =PC
=PC![]() ∵
∵![]()
∴![]() ∴
∴![]()
∴∠PQC=90![]() ∴
∴![]()
(1)由旋转的性质可得到的条件是:①BP=BQ、PA=QC,②∠ABP=∠CBQ;
由②可证得∠PBQ=∠CBP+∠CBQ=∠CBP+∠ABP=∠ABC=60°,联立BP=BQ,即可得到△BPQ是等边三角形的结论,则BP=PQ;将等量线段代换后,即可得出PQ2+QC2=PC2,由此可证得∠PQC=90°;
(2)由(1)的解题思路知:△PBQ是等腰Rt△,则PQ2=2PB2,其余过程同(1),只不过所得结论稍有不同.

练习册系列答案
相关题目