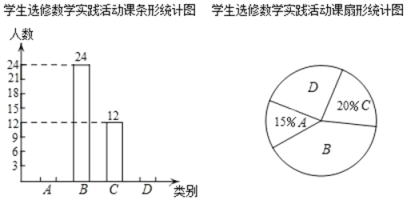
题目内容
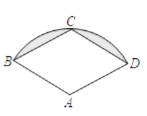
【题目】如图,已知![]() 中直径
中直径![]() ,半径
,半径![]() ,点
,点![]() 是半圆
是半圆![]() 的三等分点,点
的三等分点,点![]() 是半径
是半径![]() 上的动点,使
上的动点,使![]() 的值最小时,
的值最小时,![]() ( )
( )

A.1B.![]() C.2D.3
C.2D.3
【答案】C
【解析】
接PA.因为OC⊥直径AB,所以CO垂直平分AB.根据“垂直平分线上的点到线段两端的距离相等”得PB+PD=PA+PD,根据“两点之间线段最短”可知,连接BD,与CO相交于P,则AD的长度即为PB+PD的最小值.然后利用解直角三角形的知识求出PO的值即可.
连接PA,与CO相交于P,连接BD.
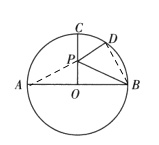
∵OC⊥AB,
∴CO垂直平分AB,
∴PA=PB,
∴PB+PD=PA+PD,
∴根据“两点之间线段最短”可知,AD的长度即为PB+PD的最小值.
∵AB为直径,
∴∠D=90°,
∵点![]() 是半圆
是半圆![]() 的三等分点,
的三等分点,
∴ ![]() 的度数为60°,
的度数为60°,
∴∠A=30°,
∴![]() ,
,
∴![]() ;
;
故答案为:C.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
【题目】某大学生利用暑假40天社会实践参与了某公司旗下一家加盟店经营,了解到一种成本为20元/件的新型商品在第![]() 天销售的相关信息如下表所示:
天销售的相关信息如下表所示:
销售量 |
|
销售单价 | 当 当 |
(1)请计算第几天该商品的销售单价为35元/件;
(2)这40天中该加盟店第几天获得的利润最大?最大利润是多少?
(3)在实际销售的前20天中,公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店![]() 元奖励,通过该加盟店的销售记录发现,前10天中,每天获得奖励后的利润随时间
元奖励,通过该加盟店的销售记录发现,前10天中,每天获得奖励后的利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.