题目内容
【题目】如图,在![]() 中,
中,![]() 以
以![]() 为直径的⊙
为直径的⊙![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线交
的切线交![]() 于点
于点![]() ,连接
,连接![]() .
.
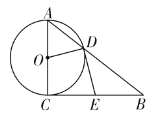
(1)求证:![]() ;
;
(2)连接![]() ,并延长
,并延长![]() 交圆
交圆![]() 于点
于点![]() ,
,![]() .
.
填空:①当![]() __________时,四边形
__________时,四边形![]() 是菱形;
是菱形;
②当![]() 的长=__________时,四边形
的长=__________时,四边形![]() 是正方形.
是正方形.
【答案】(1)详见解析;(2)①3;②![]()
【解析】
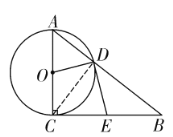
(1)连接CD,根据切线的性质,就可以证出∠B=∠BDE,从而证明BE=CE.
(2)①根据菱形的性质可得出△AOD是等边三角形,则BC=6,求出DE=3;
②由正方形的性质可得∠AOF=∠EOC=45°,则根据弧长公式可得出答案.
(1)证明:如图,连接![]() ,
,
 ,
,
![]() 为
为![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为⊙
为⊙![]() 的直径,
的直径,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ;
;
(2)①如图,
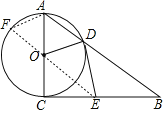
当四边形AFOD为菱形时,AF=FO=OD=AD,
∴AD=OD=AO,
∴△AOD是等边三角形,
∴∠DAC=60°,
∴![]() .
.
∴![]()
故答案为: 3;
②当四边形OCED是正方形时,如图,
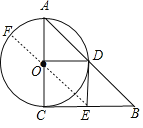
∴∠EOC=45°,
∴∠AOF=∠EOC=45°
∴弧AF的长为![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目
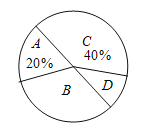
【题目】对某校学生寒假阅读时间情况调查,抽样统计绘制了两幅不完整的统计图,请结合信息解决下列问题:
阅读时间(小时) |
|
|
|
|
人数 | 60 | 80 |
(1)这次统计A类 人;D类 人;
(2)如果该校有1200学生,那么D类学生数量约为多少人?
(3)甲、乙、丙、丁4名学生是阅读属于D类学生,他们分别来自九年级1人,八年级1人,七年级2人,现抽取2人电话回访,则抽取到2人同为七年级学生的概率为多少?