题目内容
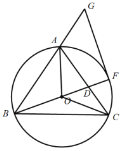
【题目】已知:如图,⊙O的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F .
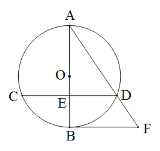
(1)求证:BF是⊙O的切线;
(2)连结BC,若⊙O的半径为2,tan∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由垂径定理可证AB⊥CD,由CD∥BF,得AB⊥BF,则BF是⊙O的切线;
(2)连接BD,根据同弧所对圆周角相等得到∠BCD =∠BAD,再利用圆的性质得到∠ADB=90°, tan∠BCD= tan∠BAD=![]() ,得到BD与AD的关系,再利用解直角三角形可以得到BD、AD与半径的关系,进一步求解即可得到答案.
,得到BD与AD的关系,再利用解直角三角形可以得到BD、AD与半径的关系,进一步求解即可得到答案.
(1)证明:∵ ⊙O的直径AB与弦CD相交于点E,且E为CD中点
∴ AB ⊥CD, ∠AED =90°
∵ CD // BF
∴ ∠ABF =∠AED =90°
∴ AB⊥BF
∵ AB是⊙O的直径
∴ BF是⊙O的切线
(2)解:连接BD
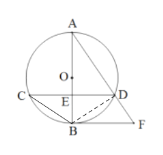
∵∠BCD、∠BAD是同弧所对圆周角
∴∠BCD =∠BAD
∵ AB是⊙O的直径
∴∠ADB=90°
∵ tan∠BCD= tan∠BAD=![]()
∴![]()
∴设BD=3x,AD=4x
∴AB=5x
∵ ⊙O的半径为2,AB=4
∴5x=4,x=![]()
∴AD=4x=![]()

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目