Question

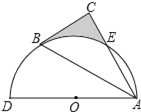
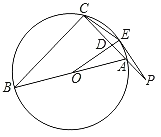
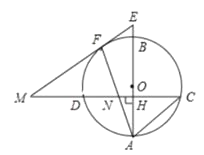
【题目】如图，已知AB是圆O的直径，弦CD⊥AB，垂足为H，在CD上有点N满足CN=CA，AN交圆O于点F，过点F的AC的平行线交CD的延长线于点M，交AB的延长线于点E．

（1）求证：EM是圆O的切线；

（2）若AC：CD=5：8，AN=3，求圆O的直径长度．

（3）在（2）的条件下，直接写出FN的长度．

Answer 1

【答案】（1）证明见解析；（2）25；（3）

【解析】

（1）连接FO，根据等边对等角可得∠CAN=∠CNA，利用两直线平行内错角相等，可得 ∠CAN=∠MFN ，从而可得∠MFN=∠FNM=∠CAN，利用直角定义可得∠MFO=90°，即证直线ME与圆O相切.

（2）根据垂径定理可得CH=DH=4a ， AH=3a.利用勾股定理可得AN的值，从而求出a=3，即得 AH、CH的值 .

设圆的半径为r，则OH=r﹣9，在Rt△OCH中，利用勾股定理可得 ， 解出r值，即得直径.

（3）连接BF，可证△ANH∽△ABF，可得 ， 代入数据可求出AF= ， 由FN=AF-AN，即得AN的长度.

（1）证明：连接FO，

∵AN=AC，

∴∠CAN=∠CNA

∵AC∥ME，

∴∠CAN=∠MFN

∵∠CNA=∠FNM

∴∠MFN=∠FNM=∠CAN

又∵CD⊥AB，

∴∠HAN+∠HNA=90°，

∵AO=FO，

∴∠OAF=∠OFA

∴∠OFA+∠MFN=90°，即∠MFO=90°，

∴直线ME与圆O相切

（2）解：连接OC，

∵AC：CD=5：8，设AC=5 a，则CD=8 a，

∵CD⊥AB，

∴CH=DH=4 a，AH=3 a，

∵CA=CN，

∴NH= a，

∴AN= ，

∴ a=3，AH=3, a=9，CH=4 ,a=12．

设圆的半径为r，则OH=r﹣9，

在Rt△OCH中，OC=r，CH=12，OH=r﹣9，

由OC2=CH2+OH2得 ，

解得：r= ，

∴圆O的直径的长度为2r=25

（3）连接BF，根据（2）

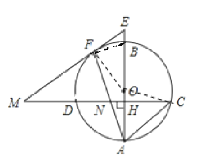
可得△ANH∽△ABF

∴可得

解得AF=

∵FN=AF-AN=-3 =

∴FN=