题目内容
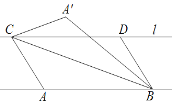
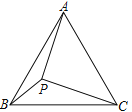
【题目】如图,在等边△ABC中,AC=7,点P在△ABC内部,且∠APC=90°,∠BPC=120°,则△APC的面积为___________
【答案】![]()
【解析】将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;
解:如图所示,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,
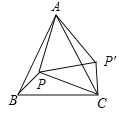
∴△APP′是等边三角形,∠AP′C=∠APB=360°90°120°=150°,
∴PP′=AP,∠AP′P=∠APP′=60°,
∴∠PP′C=90°,∠P′PC=30°,
∴PP′=![]() PC,即AP=
PC,即AP=![]() PC,
PC,
∵∠APC=90°,
∴AP2+PC2=AC2,即(![]() PC)2+PC2=72,
PC)2+PC2=72,
∴PC=![]() ,
,
∴AP=![]() ,
,
∴S△APC=![]() APPC=
APPC=![]() .
.

练习册系列答案
相关题目