题目内容
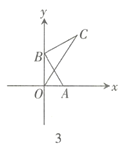
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
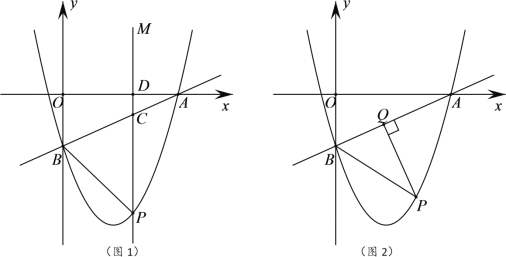
(1)求此抛物线对应的函数表达式;
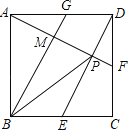
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
【答案】(1)抛物线对应的函数表达式为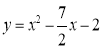 ;(2)P的坐标为
;(2)P的坐标为![]() 或
或![]() ;(3)点P的横坐标为3或
;(3)点P的横坐标为3或![]() .
.
【解析】
(1)先利用一次函数求出A,B两点的坐标,然后用待定系数法即可求出抛物线的表达式;
(2)分两种情况:若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,分情况进行讨论即可;
,分情况进行讨论即可;
(3)分两种情况,![]() 和
和![]() ,分情况进行讨论即可.
,分情况进行讨论即可.
(1)令![]() 时,
时,![]() ,
,
∴![]() ,
,
令![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() ,
,
将点A,B代入![]() 中得
中得
![]() 解得
解得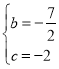
∴抛物线对应的函数表达式为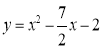 .
.
(2)设![]() ,
,
若![]() ,则
,则![]() ,
,
此时P点的纵坐标与B点的纵坐标相同,
∴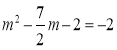 ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
∴![]() ,
,
若![]() ,则
,则![]() ,作PQ⊥OB于点Q,
,作PQ⊥OB于点Q,
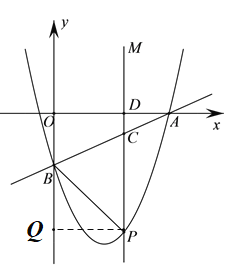
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
即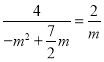 ,
,
解得![]() (舍去)或
(舍去)或![]()
∴![]()
综上所述,P的坐标为![]() 或
或![]() .
.
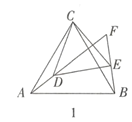
(3)若![]() ,过点B作BC∥OA交PQ于点C,过点P作PD⊥OB于点D
,过点B作BC∥OA交PQ于点C,过点P作PD⊥OB于点D
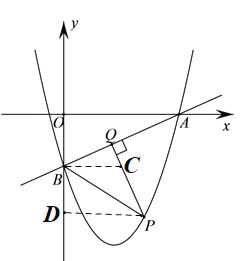
∵BC∥OA
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设![]()
∴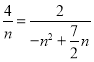
解得![]() (舍去)或
(舍去)或![]()
∴![]()
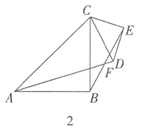
若![]() ,如图,取AB的中点E,连接OE,过P作PG⊥x轴于G,交直线AB于H,过O作OF⊥AB于F,连接AP,则∠BPQ=∠OEF,
,如图,取AB的中点E,连接OE,过P作PG⊥x轴于G,交直线AB于H,过O作OF⊥AB于F,连接AP,则∠BPQ=∠OEF,
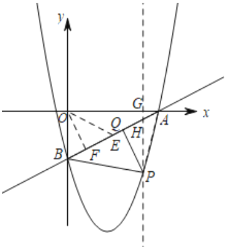
设点![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
则有![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 即
即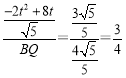 ,
,
![]()
![]() ,
,
![]() ,
,
化简得:![]() ,即
,即![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
综上,存在点P,使得△PBQ中有某个角的度数等于∠OAB度数的2倍时,其P点的横坐标为3或![]() .
.

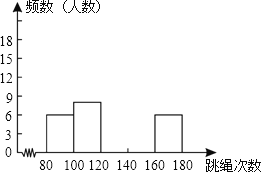
【题目】为了进一步了解某校九年级1000名学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,试估计该年级学生不合格的人数大约有多少人?
【题目】某商场经营一种商品,进价是每千克30元,根据市场调查发现,每日的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系.下表记录的是某两日的有关数据:
(元/千克)满足一次函数关系.下表记录的是某两日的有关数据:
| 35 | 40 |
| 850 | 800 |
(1)求![]() 与
与![]() 的函数关系式(不求自变量的取值范围);
的函数关系式(不求自变量的取值范围);
(2)在销售过程中销售单价不低于成本价,且不高于80元,某日该商场出售这种商品获得了14000元的利润,求该商品的售价?
(3)若某日该商场这种商品的销售量不少于500千克,求这一天该商场销售这种商品获得的最大利润为多少元?