题目内容
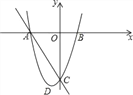
【题目】已知二次函数y=a(x﹣1)2+k的图象与x轴交于A,B两点,AB=4,与y轴交于C点,E为抛物线的顶点,∠ECO=135°.
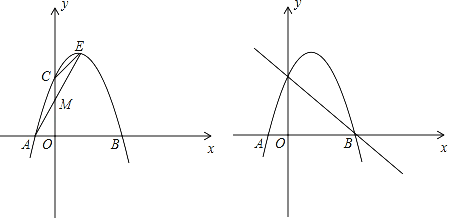
(1)求二次函数的解析式;
(2)若P在第四象限的抛物线上,连接AE交y轴于点M,连接PE交x轴于点N,连接MN,且S△EAP=3S△EMN,求点P的坐标;
(3)过直线BC上两点P,Q(P在Q的左边)作y轴的平行线,分别交抛物线于N,M,若四边形PQMN为菱形,求直线MN的解析式.
【答案】(1)y=﹣x2+2x+3;(2)P坐标为(1+![]() ,﹣2);(3)无答案.
,﹣2);(3)无答案.
【解析】
(1)根据二次函数解析式确定出对称轴为直线x=1,由A、B关于直线x=1对称且AB=4求得A、B坐标,由∠ECO=135°得到C的纵坐标为k1,把A、C坐标代入函数解析式即求得a、k的值;
(2)根据点A、E的坐标证全等可得点M是AE的中点,又△AMN与△EMN以AM、EM为底时高相等,即面积相等;由S△EAP=3S△EMN可得△NAP与△AMN面积相等,且有公共底边AN,所以高相等,进而得到点P的纵坐标为2,代入抛物线解析式即求出P的横坐标;
(3)由于直线BC上y随x的增大而减小,由条件“四边形PQMN为菱形”可得M、N必须在直线BC的同侧,其菱形必须在y轴右侧.设点P横坐标为p,点Q横坐标为p+t,则可用p、t表示M、N的坐标并把PN、PQ、MQ表示出来,根据菱形性质PN=PQ=MQ列得关于p、t的方程组,求解后讨论解是否合理即求出点P坐标.
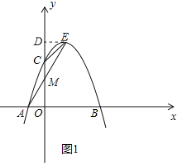
解:(1)过点E作ED⊥y轴于点D,如图1
∴∠CDE=90°
∵二次函数y=a(x﹣1)2+k的图象对称轴为直线x=1
∴xE=1,yE=k,即DE=1,OD=k
∵点A、B关于直线x=1对称,AB=4
∴A(﹣1,0),B(3,0)
∵∠ECO=135°
∴∠DCE=45°
∴CD=DE=1
∴OC=OD﹣CD=k﹣1,即yC=k﹣1
把点A(﹣1,0),C(0,k﹣1)代入二次函数解析式得:
![]() 解得:
解得:![]()
∴二次函数的解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3
(2)过P作PF⊥x轴于点F,如图2
∵A(﹣1,0),E(1,4)
∴OA=DE=1,OD=4
在△AOM与△EDM中,
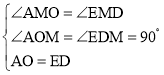 ,
,
∴△AOM≌△EDM(AAS)
∴AM=EM,OM=DM=![]() OD=2
OD=2
∴S△AMN=S△EMN
∵S△EAP=3S△EMN
∴S△NAP=S△EAP﹣S△AMN﹣S△EMN=3S△EMN﹣2S△EMN=S△EMN=S△AMN
∴PG=OM=2
∵点P在第四象限
∴yP=﹣(x﹣1)2+4=﹣2
解得:x1=![]() ,x2=
,x2=![]() (舍去)
(舍去)
∴点P坐标为(![]() ,﹣2)
,﹣2)
(3)∵四边形PQMN为菱形
∴PQ∥MN,PN=PQ=MQ=MN
∴点M、N必须同时在直线BC的上方或下方
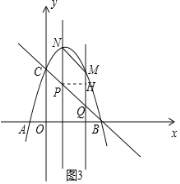
过点P作PH⊥QM于点H,如图3
∵B(3,0),C(0,3)
∴直线BC解析式为y=﹣x+3,y随x的增大而减小
∴PQ不可能在y轴左侧
设P(p,﹣p+3),Q(p+t,﹣p﹣t+3)(p>0,t>0)
∴PH=t,HQ=﹣p+3﹣(﹣p﹣t+3)=t
∴PQ=![]()
∵点M、N在二次函数y=﹣x2+2x+3图象上
∴N(p,﹣p2+2p+3),M(p+t,﹣(p+t)2+2(p+t)+3)
∴PN=|﹣p2+2p+3﹣(﹣p+3)|=|﹣p2+3p|,
MQ=|﹣(p+t)2+2(p+t)+3)﹣(﹣p﹣t+3)|=|﹣p2﹣2pt﹣t2+3p+3t|
且两绝对值号里的式子同正同负
∴﹣p2+3p=﹣p2﹣2pt﹣t2+3p+3t=![]()
解得: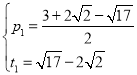 ,
,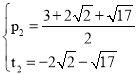 (舍去),
(舍去),
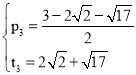 (舍去),
(舍去), (舍去),
(舍去),
∴﹣p+3=![]()
∴点P坐标为(![]() ,
,![]() ).
).


【题目】为了加强学生安全教育,某市某中学举行了一次“安全知识竞赛”,共有1600名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面的频数分布表和频数分布直方图,解答下列问题:
频数分布表
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 12 | 0.24 |
80.5~90.5 | 15 | 0.30 |
90.5~100.5 | a | b |
合计 |
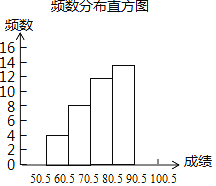
(1)频数分布表中a= ,b= ;
(2)抽取的样本容量是 ,请补全频数分布直方图.
(3)若成绩在80分以上(不含80分)为优秀,则该校成绩没达到优秀的约为多少人?
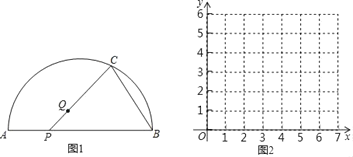
【题目】如图,点P是![]() 所对弦AB上一动点,点Q是
所对弦AB上一动点,点Q是![]() 与弦AB所围成的图形的内部的一定点,作射线PQ交
与弦AB所围成的图形的内部的一定点,作射线PQ交![]() 于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
小平根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小平的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.37 | 4.06 | 2.83 | m | 3.86 | 4.83 | 5.82 |
y2/cm | 2.68 | 3.57 | 4.90 | 5.54 | 5.72 | 5.79 | 5.82 |
经测量m的值是(保留一位小数).
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△BCP为等腰三角形时,AP的长度约为 cm.