题目内容
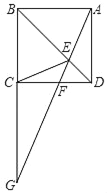
【题目】如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F.
(1)求证:四边形ABCD是正方形;
(2)当AE=3EF,DF=1时,求GF的值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由∠BAE=∠BCE,∠AED=∠CED,利用三角形外角的性质,即可得∠CBE=∠ABE,又由四边形ABCD是矩形,即可证得△ABD与△BCD是等腰直角三角形,继而证得四边形ABCD是正方形;
(2)在正方形ABCD中,AB∥CD,得到△AEB∽△FED,求得![]() ,于是得到AB=3DF=3,由正方形的性质得到CD=AD=AB=3,求出CF=CD﹣DF=3﹣1=2,通过△ADF∽△GCF,得到
,于是得到AB=3DF=3,由正方形的性质得到CD=AD=AB=3,求出CF=CD﹣DF=3﹣1=2,通过△ADF∽△GCF,得到![]() ,于是得到CG=2AD=6,根据勾股定理即可得到结论.
,于是得到CG=2AD=6,根据勾股定理即可得到结论.
(1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90°,
∵∠BAE=∠BCE,
∴∠BAD﹣∠BAE=∠BCD﹣∠BCE,
即∠DAE=∠DCE,
在△AED和△CED中,
 ,
,
∴△AED≌△CED(AAS),
∴AD=CD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形;
(2)在正方形ABCD中,AB∥CD,
∴△AEB∽△FED,
∴![]() ,
,
∵AE=3EF,DF=1,
∴AB=3DF=3,
∴CD=AD=AB=3,
∴CF=CD﹣DF=3﹣1=2,
∵AD∥CG,
∴△ADF∽△GCF,
∴![]() ,
,
∴CG=2AD=6,
在Rt△CFG中,GF=![]() .
.

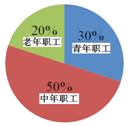
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | <>60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
(1)扇形统计图中老年职工所占部分的圆心角度数为
(2)小张、小王和小李三人中, 的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.