题目内容
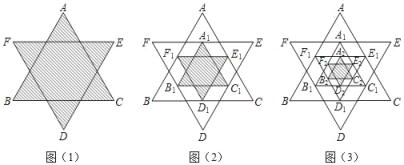
【题目】如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
先分别求出第一个正六角星形AFBDCE与第二个边长之比,再根据相似多边形面积的比等于相似比的平方,找出规律即可解答.
∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1且相似比为2:1,
∵正六角星形AFBDCE的面积为1,
∴正六角星形A1F1B1D1C1E1的面积为![]() ,
,
同理可得,第二个六角形的面积为:![]() ,
,
第三个六角形的面积为:![]() ,
,
第四个六角形的面积为:![]() ,
,
故选D.

练习册系列答案
相关题目