题目内容
【题目】综合题 ——
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.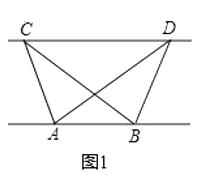
(2)结论应用:
①如图2,点M、N在反比例函数y= ![]() (k>0)的图象上,过点M作ME⊥y轴,垂足分别为E,F,试证明:MN∥EF;
(k>0)的图象上,过点M作ME⊥y轴,垂足分别为E,F,试证明:MN∥EF;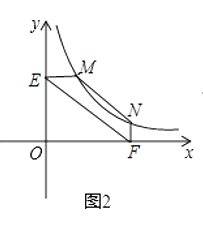
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.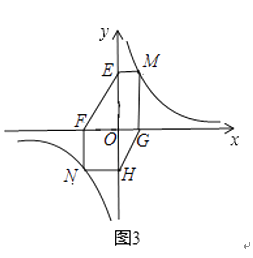
【答案】
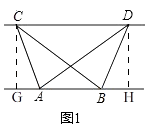
(1)解:如图1,过点C作⊥AB于G,过点D作DH⊥AB于H,
∴∠CGA=∠DHB=90°,
∴CG∥DH,
∵△ABC和△ABD的面积相等,
∴CG=DH,
∴四边形CGHD是平行四边形、
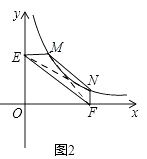
(2)解:①如图2,连接MF,NE,
设M(x1,y1),N(x2,y2),
∵点M,N在反比例函数y= ![]() (k>0)的图象上,
(k>0)的图象上,
∴x1y1=k,x2y2=k,
∵ME⊥y轴,NF⊥x轴,
∴OE=y1,OF=x2,
∴S△EFM= ![]() x1x2=
x1x2= ![]() k,S△EFN=
k,S△EFN= ![]() x2y2=
x2y2= ![]() k,
k,
∴S△EFM=S△EFN,
由(1)中的结论可知,MN∥EF;
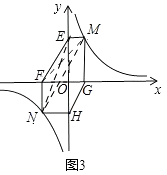
②MN∥EF,理由:如图3,由(1)中的结论可知,MN∥EF.
【解析】(1)过点C作⊥AB于G,过点D作DH⊥AB于H,根据△ABC和△ABD的面积相等,去证明CG∥DH,CG=DH即可证得结论。
(2)连接MF,NE,先证明S△EFM=S△EFN,然后利用(1)的结论得证。
【考点精析】掌握平行线之间的距离和三角形的面积是解答本题的根本,需要知道两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;三角形的面积=1/2×底×高.

练习册系列答案
相关题目