题目内容
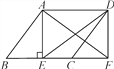
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先证明四边形AEFD是平行四边形,再证明∠AEF=90°即可.
(2)证明△ABF是直角三角形,由三角形的面积即可得出AE的长.
试题解析:(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即EF=BC.
∵在ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.
∵AE⊥BF,
∴△ABF的面积=![]() ABAF=
ABAF=![]() BFAE.
BFAE.
∴AE=![]() .
.

练习册系列答案
相关题目
【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).