题目内容
【题目】在
中，射线
平分
交
于点
，点
在边上运动（不与点重合），过点作
交
于点
.
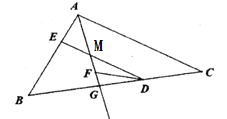
（1）如图1，点在线段
上运动时，
平分
.
①若
，
，则
_____；若
，则_____；
②试探究
与
之间的数量关系？请说明理由；
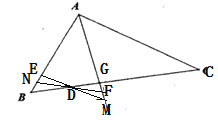
（2）点在线段
上运动时，
的角平分线所在直线与射线交于点
.试探究与之间的数量关系，并说明理由.
【答案】（1）①115°，110°；②
，证明见解析；（2）
，证明见解析.
【解析】
（1）①根据角平分线的定义求得∠CAG=
∠BAC=50°；再由平行线的性质可得∠EDG=∠C=30°，∠FMD=∠GAC=50°；由三角形的内角和定理求得∠AFD的度数即可；已知AG平分∠BAC，DF平分∠EDB，根据角平分线的定义可得∠CAG=∠BAC，∠FDM=∠EDG；由DE//AC，根据平行线的性质可得∠EDG=∠C，∠FMD=∠GAC；即可得∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=（∠BAC+∠C）=×140°=70°；再由三角形的内角和定理可求得∠AFD=110°；②∠AFD=90°+∠B，已知AG平分∠BAC，DF平分∠EDB，根据角平分线的定义可得∠CAG=∠BAC，∠FDM=∠EDG；由DE//AC，根据平行线的性质可得∠EDG=∠C，∠FMD=∠GAC；由此可得∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=（∠BAC+∠C）=×（180°-∠B）=90°-∠B；再由三角形的内角和定理可得∠AFD=90°+∠B；（2）∠AFD=90°-∠B，已知AG平分∠BAC，DF平分∠EDB，根据角平分线的定义可得∠CAG=∠BAC，∠NDE=∠EDB，即可得∠FDM=∠NDE=∠EDB；由DE//AC，根据平行线的性质可得∠EDB=∠C，∠FMD=∠GAC；即可得到∠FDM=∠NDE=∠C，所以∠FDM +∠FMD =∠C+∠BAC=（∠BAC+∠C）=×（180°-∠B）=90°-∠B；再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-∠B.
（1）①∵AG平分∠BAC，∠BAC=100°，
∴∠CAG=∠BAC=50°；
∵
，∠C=30°，
∴∠EDG=∠C=30°，∠FMD=∠GAC=50°；
∵DF平分∠EDB，
∴∠FDM=∠EDG=15°；
∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°；
∵∠B=40°，
∴∠BAC+∠C=180°-∠B=140°；
∵AG平分∠BAC，DF平分∠EDB，
∴∠CAG=∠BAC，∠FDM=∠EDG，
∵DE//AC，
∴∠EDG=∠C，∠FMD=∠GAC；
∴∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=（∠BAC+∠C）=×140°=70°；
∴∠AFD=180°-（∠FDM +∠FMD）=180°-70°=110°；
故答案为：115°，110°；
②∠AFD=90°+∠B，理由如下：
∵AG平分∠BAC，DF平分∠EDB，
∴∠CAG=∠BAC，∠FDM=∠EDG，
∵DE//AC，
∴∠EDG=∠C，∠FMD=∠GAC；
∴∠FDM +∠FMD=∠EDG +∠GAC=∠C+∠BAC=（∠BAC+∠C）=×（180°-∠B）=90°-∠B；
∴∠AFD=180°-（∠FDM +∠FMD）=180°-（90°-∠B）=90°+∠B；
（2）∠AFD=90°-∠B，理由如下：
如图，射线ED交AG于点M，
∵AG平分∠BAC，DF平分∠EDB，
∴∠CAG=∠BAC，∠NDE=∠EDB，
∴∠FDM=∠NDE=∠EDB，
∵DE//AC，
∴∠EDB=∠C，∠FMD=∠GAC；
∴∠FDM=∠NDE=∠C，
∴∠FDM +∠FMD =∠C+∠BAC=（∠BAC+∠C）=×（180°-∠B）=90°-∠B；
∴∠AFD=∠FDM +∠FMD=90°-∠B.
