题目内容
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求: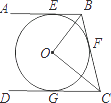
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
【答案】
(1)解:连接OF;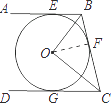
根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°
(2)解:由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC= ![]() =10cm,
=10cm,
∴BE+CG=BC=10cm
(3)解:∵OF⊥BC,
∴∠BFO=∠OFC=90°
∵∠BOC=90°
∴∠BOF+∠COF=90°,∠COF+∠FCO=90°。
∴∠BOF=∠FCO
∴△FCO∽△FOB
∴![]()
∴OF= ![]() =4.8cm
=4.8cm
【解析】(1)根据已知圆的切线,因此连接OF,根据切线长定理得出∠OBF=∠OBE,∠OCF=∠OCG,再根据平行线的性质证得∠ABC+∠BCD=180°,再证明∠OBE和∠OCF互余,即可求出∠BOC的度数。
(2)根据切线长第得出BE=BF,CF=CG,再在Rt△OBC中,利用勾股定理求出BC的长,然后根据BC=BF+CF=BE+CG,计算即可得出答案。
(3)先证明∠BOF=∠FCO,再证明△FCO∽△FOB,然后利用相似三角形的性质得出对应边成比例,即可求出OF的长。
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目