题目内容
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)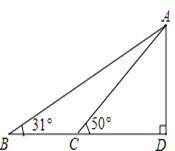
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
【答案】
(1)解:在Rt△ABD中,
∵AD=24m,∠B=31°,
∴tan31°= ![]() ,
,
即BD= ![]() =40m,
=40m,
在Rt△ACD中,
∵AD=24m,∠ACD=50°,
∴tan50°= ![]() ,
,
即CD= ![]() =20m,
=20m,
∴BC=BD﹣CD=40﹣20=20m,
即B,C的距离为20m.
(2)解:根据题意得:
20÷2=10m/s<15m/s,
即此轿车没有超速.
【解析】(1)在Rt△ABD中,根据锐角三角函数定义可得BD=AD·tan31°=40m,在Rt△ACD中,根据锐角三角函数定义可得CD=AD·tan50°=20m,再由BC=BD﹣CD即可得出B,C的距离.
(2)根据速度=路程÷时间,再与15m/s比较即可得出此轿车有没有超速.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目