Question

【题目】如图，直线AB、CD、BC分别与⊙O相切于E、F、G，且AB∥CD，若OB=6cm，OC=8cm，则BE+CG的长等于（ ）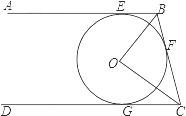

A.13
B.12
C.11
D.10

Answer 1

【答案】D
【解析】解：∵AB∥CD，
∴∠ABC+∠BCD=180°，
∵CD、BC，AB分别与⊙O相切于G、F、E，
∴∠OBC= ∠ABC，∠OCB= ∠BCD，BE=BF，CG=CF，
∴∠OBC+∠OCB=90°，
∴∠BOC=90°，
∴BC= =10，
∴BE+CG=10（cm）．
故答案为：D．
根据平行线的性质证得∠ABC+∠BCD=180°，再根据切线长定理得出BE=BF，CG=CF，∠OBC= ∠ABC，∠OCB= ∠BCD，就可证明∠BOC=90°，然后根据勾股定理求出BC的长，再证明BC=BE+CG，即可得出答案。