题目内容
【题目】如图,AD为⊙O直径,作⊙O的内接正三角形ABC,下列作法错误的是( )
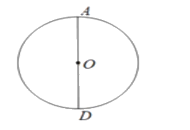
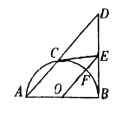
A.作OD的中垂线,交⊙O于B,C,连结AB,AC;
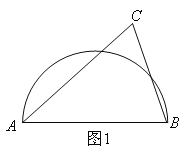
B.以D点为圆心,OD长为半径作圆弧,交圆于点B,C,连结AB, BC,CA;
C.以A点为圆心,AO长为半径作圆弧,交圆于点E,F,再分别以E,F为圆心,AO长为半径作圆弧,交圆于不同于点A的两点B,C,连结AB,BC,CA
D.作AD的中垂线,交⊙O于B,C,连结AB,AC
【答案】D
【解析】
直接利用等边三角形的判定与性质分别分析得出答案.
连接OB、OC,如图1.
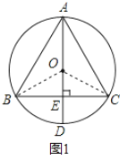
由作图可知:BC是半径OD的垂直平分线,
∵AD为⊙O的直径,
∴![]() ,
,![]() ,
,![]() ,
,
∴AB=AC.
在Rt△OEC中,
∴![]() ,
,
∴∠EOC=60°,
∴∠BOC=120°,
∴∠BAC=60°,
∴△ABC是等边三角形,故A作图正确,不符合题意;
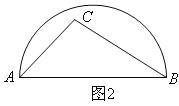
如图2,连接DB、DC.
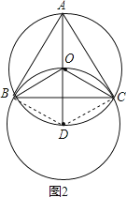
由作图可知:DB=DO=DC,
在⊙O中,OB=OD=OC,
∴△OBD和△OCD都是等边三角形,
∴∠ODB=∠ODC=60°,
∵![]() ,
,
∴∠ODB=∠ACB=∠ABC=∠ODC=60°,
∴△ABC是等边三角形, 故B作图正确,不符合题意;
连接AE,EO,BE,BO,AF,FO,CO,CF,
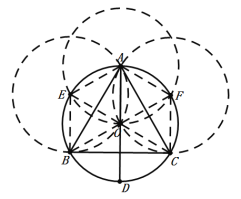
由作图可知:AE=EO=BE=BO=AF=FO=CO=CF=AO,
∴△OAE、△OBE、△OAF、△OCF都是等边三角形,
∴∠AOB=∠AOC=60°+60°=120°,
∴∠BOC=360°-∠AOB=∠AOC=120°,
∵BO =CO =AO,
∴△AOB![]() △AOC
△AOC![]() △BOC,
△BOC,
∴AB=AC=BC,
∴△ABC是等边三角形, 故C作图正确,不符合题意;
由作图可知:OB=OC=OA=OD,
∴△ABC是等腰直角三角形,故D作图错误,符合题意.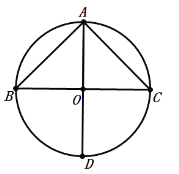
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目