Question

【题目】如图，一垂直于地面的灯柱AB被一钢筋CD固定，CD与地面成45°夹角（∠CDB=45°），在C点上方2米处加固另一条钢线ED，ED与地面成53°夹角（∠EDB=53°），那么钢线ED的长度约为多少米？（结果精确到1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）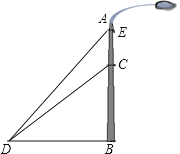

Answer 1

【答案】解：设BD=x米，则BC=x米，BE=（x+2）米，
在Rt△BDE中，tan∠EDB= ，
即 ，
解得，x≈6.06，
∵sin∠EDB= ，
即0.8= ，
解得，ED≈10
即钢线ED的长度约为10米
【解析】根据题意，可以得到BC=BD，由∠CDB=45°，∠EDB=53°，由三角函数值可以求得BD的长，从而可以求得DE的长．本题考查解直角三角形的应用，解题的关键是明确题意，利用三角函数值求出相应的边的长度．