题目内容
【题目】我市劲威乡A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
【1】请填写下表

【2】求出yA、yB与x之间的函数解析式;
【3】试讨论A、B两村中,哪个村的运费最少;
【4】考虑B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
【答案】
【1】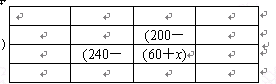
【2】∵yA=20x+25(200-x),∴yA=-5x+5000
又∵yB=15(240-x)+18(60+x),∴yB=3x+4680
【3】当5000-5x≤4680+3x时,即:40<x≤200时,yA<yB,A村运费较少
当5000-5x=4680+3![]() x时,即:x=40时,yA=yB,∴两村运费一样
x时,即:x=40时,yA=yB,∴两村运费一样
当5000-5x>4680+3x时,即:x<40时,B村运费较少
【4】由题意知:yB=3x+4680≤4830,∴x≤50
∵y=yA+yB=-5x+5000+3x+4680=-2x+9680,∴y随x增大而减小
当x=50时,y有最小值,![]() =9580(元)
=9580(元)
即由A村运往C库50吨,运D库150吨,而B村运往C库190吨,运D库110吨则两村运费之和最小,为9580元
【解析】(1)利用运送的吨数×每吨运输费用=总费用,列出函数解析式即可解答;
(2)由(1)中的函数解析式联立方程与不等式解答即可;
(3)首先由B村的荔枝运费不得超过4830元得出不等式,再由两个函数和,根据自变量的取值范围,求得最值.
解:(1)A,B两村运输荔枝情况如表,
收收地地运运地地 | C | D | 总计 |
A | x吨 | 200-x | 200吨 |
B | 240-x | x+60 | 300吨 |
总计 | 240吨 | 260吨 | 500吨 |
yA=20x+25(200-x)=5000-5x,
yB=15(240-x)+18(x+60)=3x+4680;
(2)①当yA=yB,即5000-5x=3x+4680,
解得x=40,
当x=40,两村的运费一样多,
②当yA>yB,即5000-5x>3x+4680,
解得x<40,
当0<x<40时,A村运费较高,
③当yA<yB,即5000-5x<3x+4680,
解得x>40,
当40<x≤200时,B村运费较高;
(3)B村的荔枝运费不得超过4830元,
yB=3x+4680≤4830,
解得x≤50,
两村运费之和为yA+yB=5000-5x+3x+4680=9680-2x,
要使两村运费之和最小,所以x的值取最大时,运费之和最小,
故当x=50时,最小费用是9680-2×50=9580(元).

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有名学生参加;
(2)直接写出表中a= , b=;
(3)请补全下面相应的频数分布直方图;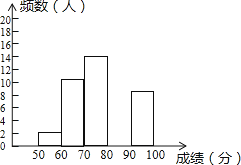
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .