题目内容
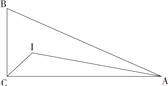
【题目】如图,Rt△ABC中,∠ACB=90°,BC=5,AC=12,I是Rt△ABC的内心,连接CI,AI,则△CIA外接圆的半径为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】过I作ID⊥AC于D,设△CIA的外接圆为⊙O,连接CO,IO,AO.
由勾股定理得到AB的长.由公式直角三角形内切圆半径=(a+b-c)÷2,得到内切圆半径ID的长,由CD=ID,得到CD的长.以C为坐标原点,CA所在直线为x轴,向右为正方向,CB所在直线为y轴,向上为正方向建立直角坐标系,则C(0,0),I(2,2)A(12,0).设O(x,y),由OC=OI=OA,用两点间距离公式列方程组,求解即可得到O的坐标,即可得到结论.
过I作ID⊥AC于D,设△CIA的外接圆为⊙O,连接CO,IO,AO.
∵∠ACB=90°,BC=5,AC=12,∴AB=13.
∵I是Rt△ABC的内心,ID⊥AC,∴ID为内切圆半径,ID=(5+12-13)÷2=2,∴CD=ID=2.以C为坐标原点,CA所在直线为x轴,向右为正方向,CB所在直线为y轴,向上为正方向建立直角坐标系,则C(0,0),I(2,2)A(12,0).设O(x,y).
∵OC=OI=OA,∴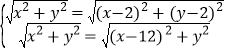 ,解得:
,解得:![]() ,∴O(6,-4),∴△CIA外接圆的半径=CO=
,∴O(6,-4),∴△CIA外接圆的半径=CO=![]() =
=![]() .
.
故选C.


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目