题目内容
【题目】如图，正方形ABCD中（各边都相等，各角都为直角），E为射线BC上一动点，点B关于直线AE的对称点为
，射线
与射线CD相交于点F．设
，
．
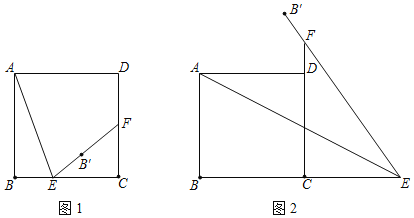
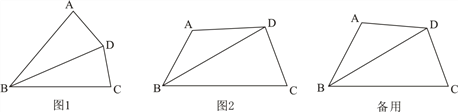
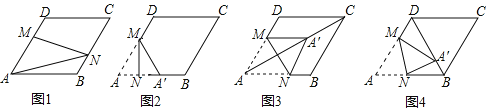
（1）如图1，正方形ABCD的边长为20，当点E在边BC上运动（点E与B、C不重合）时）：
①
的周长始终不变，请你求出这个不变的值；
②当
时，求y的值及的面积.
（2）如图2，当点E在边BC延长线上时，
①猜想BE、EF、DF之间的数量关系是__________.
②求证：的面积
.
【答案】（1）①40；②
，
；（2）①
；②见解析.
【解析】
（1）①证明
，
即可解决问题.
②求出EC、CF即可解决问题.
（2）①结论：BE﹣EF=DF.理由全等三角形的性质即可证明.
②设正方形的边长为a,利用勾股定理可得：
，在利用三角形的面积公式，化简计算即可.
解：（1）①如图1中，连接
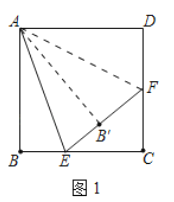
∵B、
关于直线AE对称
∴
∵AE=AE
∴
∴
∴
∵
∴
∴
∴
∴
是定值，这个值是40.
②当
时，
在
∴
解得
∴
∴
（2）①结论：BE﹣EF=DF
理由：如图2中，连接AF、
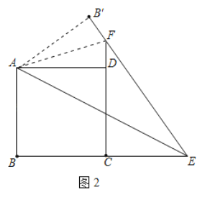
∵B、 关于直线AE对称
∴
∵AE=AE
∴
∴
∴
∵
∴
∴
∴
故答案为
②设正方形的边长为a
∵
在
∴
∴
练习册系列答案
相关题目
