题目内容
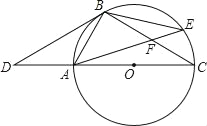
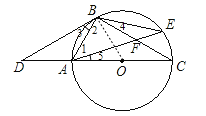
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)证明:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为16,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
【答案】(1)证明见解析;(2)36.
【解析】(1)BD是⊙O的切线.先连接OB,由于AC是直径,那么∠ABC=90°,于是∠1+∠C=90°,而OA=OB,可得∠1=∠2,结合∠3=∠C,易得∠2+∠3=90°,从而可证DB是⊙O的切线;
(2)由于cos∠BFA=![]() ,那么
,那么![]() ,利用圆周角定理可知∠E=∠C,∠4=∠5,易证△EBF∽△CAF,于是
,利用圆周角定理可知∠E=∠C,∠4=∠5,易证△EBF∽△CAF,于是![]() ,从而易求△ACF的面积.
,从而易求△ACF的面积.
(1)BD是⊙O的切线.理由如下:
如图所示,连接OB.
∵AC是⊙O的直径,∴∠ABC=90°,∴∠1+∠C=90°.
∵OA=OB,∴∠1=∠2,∴∠2+∠C=90°.
∵∠3=∠C,∴∠2+∠3=90°,∴DB是⊙O的切线;
(2)在Rt△ABF中.
∵cos∠BFA=![]() .
.
∵∠E=∠C,∠4=∠5,∴△EBF∽△CAF,
∴![]() ,即
,即![]() ,解得:S△ACF=22.5.
,解得:S△ACF=22.5.

【题目】某超市对![]() ,
,![]() 两种商品开展春节促销活动,活动方案有如下两种:
两种商品开展春节促销活动,活动方案有如下两种:
商品 |
|
| |
标价(单位:元) | 120 | 150 | |
方案一 | 每件商品出售价格 | 按标价打7折 | 按标价打 |
方案二 | 若所购商品超过10件(不同商品可累计)时,每件商品均按标价打8折后出售. | ||
(同一种商品不可同时参与两种活动)
(1)某单位购买![]() 商品5件,
商品5件,![]() 商品4件,共花费960元,求
商品4件,共花费960元,求![]() 的值;
的值;
(2)在(1)的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
【题目】为弘扬中华民族传统文化,某校举办了“燕城诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 |
| 16 |
第2组 |
|
|
第3组 |
| 20 |
第4组 |
|
|
第5组 |
| 6 |
请根据以上信息,解答下列问题:
(1)此次随机抽取的学生数是 人,![]() ,
,![]() ;
;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1500名学生,那么成绩低于70分的约有多少人?