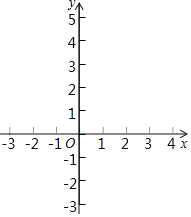题目内容
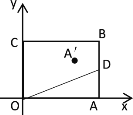
【题目】如图,在平面直角坐标系中,直线![]() 分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.
分别与x、y轴交于A、B两点,将直线AB沿着y轴翻折,交x轴负半轴于点C.
(1)求直线BC的函数关系式;
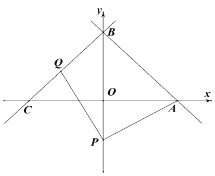
(2)点P(0,t)在y轴负半轴上,Q为线段BC上一动点(不与B、C重合).连接PA、PQ,PQ=PA
①若点Q为BC中点,求t的值;
②用t的代数式表示点Q的坐标和直线PQ的函数关系式;
③若M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,求n的取值范围.
【答案】(1)![]() ;(2)①t=-3,②
;(2)①t=-3,②![]() ,③-6<t<0,
,③-6<t<0,![]() ≤n<70
≤n<70
【解析】
(1)根据题意求出A,B的坐标,从而可得出C点的坐标,用待定系数法即可得出解析式;
(2)①首先根据Q为BC中点,得出Q的坐标,然后过Q点作QE⊥y轴,可得QE=3,EP=3-t,OP=|t|,OA=6,然后根据PQ=PA和勾股定理,可得![]() =
=![]() ,求解即可;
,求解即可;
②设Q(a,a+6),由题意得:![]() ,解出方程求出Q的坐标为(t,t+6),然后利用待定系数法求出解析式即可;
,解出方程求出Q的坐标为(t,t+6),然后利用待定系数法求出解析式即可;
③将M(2m,n-8),N(t3+2t2-2m,n)代入PQ的函数关系式得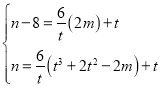 ,然后消去m得n=3t2+7t+4,在根据t的取值范围即可推出,n的取值范围.
,然后消去m得n=3t2+7t+4,在根据t的取值范围即可推出,n的取值范围.
(1)∵直线![]() 分别与x、y轴交于A、B两点,
分别与x、y轴交于A、B两点,
∴可得A(6,0),B(0,6),
∵点C和点A关于x轴对称,
∴C(-6,0),
设BC的解析式为y=kx+b,
将B,C两点代入得![]() ,
,
解得:k=1,b=6,
∴BC的解析式为:![]() ;
;
(2)①∵Q为BC中点,
∴Q的坐标为(-3,3),
过Q点作QE⊥y轴,
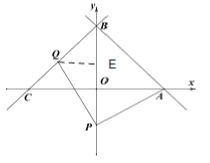
∴E的坐标为(0,3),
∴QE=3,EP=3-t,OP=|t|,OA=6,
∵PQ=PA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得t=-3;
②设Q(a,a+6),
由题意得:![]() ,
,
解得![]() ,
,![]() (舍),
(舍),
∴Q(t,t+6),
设直线PQ函数关系式为y=kx+b,
将Q,P代入得![]() ,
,
解得![]() ,
,
∴直线PQ函数关系式为![]() ;
;
③∵点M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,
由②可得PQ函数关系式为![]() ,
,
∴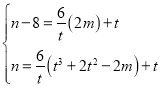 ,
,
消去m得n=3t2+7t+4,
∵Q为线段BC上一动点(不与B、C重合),
∴-6<t<0,
∵n=3t2+7t+4,
∴对称轴为t=![]() ,
,
∴n的最小值为:n=3×![]() -7×
-7×![]() +4=
+4=![]() ,
,
当t=-6时,n=3×36-7×6+4=70,
当t=0时,n=4,
∴n的取值范围是:![]() ≤n<70.
≤n<70.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案