题目内容
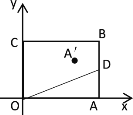
【题目】如图，在平面直角坐标系中，矩形
的点
坐标为
，点
在
轴上，点
在
轴上．点
是边
上的动点，连接
，作点关于线段的对称点
．已知一条抛物线
经过
三点，且点恰好是抛物线的顶点，则
的值为（）
A.
B.
C.
D.
【答案】B
【解析】
根据题意可得OA=8，AB=6，然后画出对应的图形，求出OE和
，根据勾股定理即可求出
，从而求出点
的坐标，设该抛物线的解析式为
，将点O的坐标代入解析式中即可求出抛物线的解析式，变为一般式即可求出结论．
解：∵矩形
的点
坐标为
，
∴OA=8，AB=6
∵抛物线
经过
三点，且点恰好是抛物线的顶点，
∴必在抛物线的对称轴上，且点O和点A关于抛物线的对称轴对称，如下图所示，设抛物线的对称轴交x轴于点E，
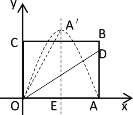
∴OE=
=4
∵点
关于线段
的对称点
∴=OA=8
由勾股定理可得
=
∴点的坐标为（4，）
设该抛物线的解析式为
将点O的坐标代入，得
解得：
∴抛物线的解析式为
∴b=
故选B．
练习册系列答案
相关题目
