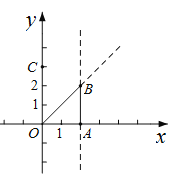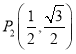Question

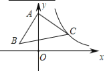
【题目】在平面直角坐标系 xOy 中，直线 l：与 x 轴交于点 A（-2，0），与 y 轴交于点 B．双曲线与直线 l 交于 P，Q 两点，其中点 P 的纵坐标大于点 Q 的纵坐标．

（1）求点 B 的坐标；

（2）当点 P 的横坐标为 2 时，求 k 的值；

（3）连接 PO，记△POB 的面积为 S，若 ，直接写出 k 的取值范围．

Answer 1

【答案】（1）（0，2）；（2）8；（3）≤k≤3或-1≤k≤．

【解析】

（1）根据点A的坐标，可求出直线的解析式，再由解析式求出B点坐标．
（2）把点P的横坐标代入直线解析式即可求得点P的纵坐标，然后把点P代入反比例函数解析式即可得k值．
（3）根据△POB的面积为S的取值范围求点P的横坐标取值，然后把横坐标代入直线解析式，即可求得点P纵坐标的取值范围，进而求得k的取值范围．

解：（1）∵直线l：y＝x＋b与x轴交于点A（2，0）
∴2＋b＝0
∴b＝2
∴一次函数解析式为：y＝x＋2

当x=0时，y=2，
∴直线l与y轴交于点B为（0，2）
∴点B的坐标为（0，2）；
（2）∵双曲线与直线l交于P，Q两点，
∴点P在直线l上
∴当点P的横坐标为2时，y＝2＋2＝4
∴点P的坐标为（2，4）
∴k＝2×4＝8
∴k的值为8；
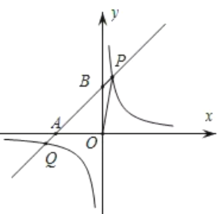
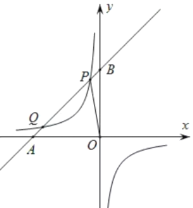
（3）如图所示，

①当k＞0时，
S＝×2×xp＝xp，
∵≤S≤1，
∴≤xp≤1，

∵点P在直线y＝x＋2上，

∴≤yp≤3，

∵点P在反比例函数，

∴xy=k，

∴≤k≤3，

②当k＜0时，
S＝×2×|xp|＝xp，
∵≤S≤1，

∴≤-xp≤1，

∴-1≤xp≤

∵点P在直线y＝x＋2上，

∴1≤yp≤，

∵点Pspan>在反比例函数，

∴xy=k，

∴-1≤k≤，
综上所述，k的取值范围为：≤k≤3或-1≤k≤．