МвДҝДЪИЭ
ЎҫМвДҝЎҝФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬Йи
Ј¬Йи![]() Ј¬
Ј¬![]() Ј®
Ј®
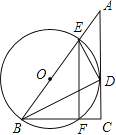
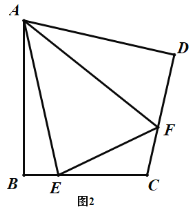
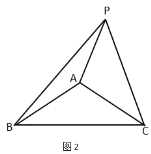
ЈЁ1Ј©ИзНј1Ј¬өұөг![]() ФЪ
ФЪ![]() ДЪЈ¬
ДЪЈ¬
ўЩИф![]() Ј¬Зу
Ј¬Зу![]() өД¶ИКэЈ»
өД¶ИКэЈ»
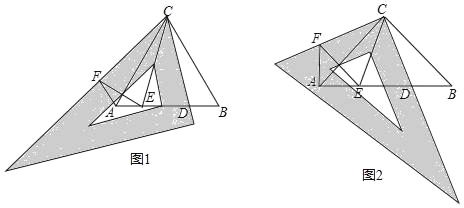
РЎГчН¬С§НЁ№э·ЦОцТСЦӘМхјю·ўПЦЈә![]() КЗ¶ҘҪЗОӘ
КЗ¶ҘҪЗОӘ![]() өДөИСьИэҪЗРОЈ¬ЗТ
өДөИСьИэҪЗРОЈ¬ЗТ![]() Ј¬ҙУ¶шИЭТЧБӘПлөҪ№№ФмТ»ёц¶ҘҪЗОӘ
Ј¬ҙУ¶шИЭТЧБӘПлөҪ№№ФмТ»ёц¶ҘҪЗОӘ![]() өДөИСьИэҪЗРОЈ®УЪКЗЈ¬Лы№эөг
өДөИСьИэҪЗРОЈ®УЪКЗЈ¬Лы№эөг![]() Чч
Чч![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ј¬·ўПЦБҪёцІ»Н¬өДИэҪЗРОИ«өИЈә______
Ј¬·ўПЦБҪёцІ»Н¬өДИэҪЗРОИ«өИЈә______![]() _______ФЩАыУГИ«өИИэҪЗРОј°өИСьИэҪЗРОөДПа№ШЦӘК¶ҝЙЗуіц
_______ФЩАыУГИ«өИИэҪЗРОј°өИСьИэҪЗРОөДПа№ШЦӘК¶ҝЙЗуіц![]() өД¶ИКэ
өД¶ИКэ
ЗлАыУГРЎНхН¬С§·ЦОцөДЛјВ·Ј¬НЁ№эјЖЛгЗуөГ![]() өД¶ИКэОӘ_____Ј»
өД¶ИКэОӘ_____Ј»
ўЪРЎНхФЪўЩөД»щҙЎЙПҪшТ»ІҪҪшРРМҪЛчЈ¬·ўПЦ![]() Ц®јдҙжФЪТ»ЦЦМШКвөДөИБҝ№ШПөЈ¬ЗлРҙіцХвёцөИБҝ№ШПөЈ¬ІўјУТФЦӨГчЈ®
Ц®јдҙжФЪТ»ЦЦМШКвөДөИБҝ№ШПөЈ¬ЗлРҙіцХвёцөИБҝ№ШПөЈ¬ІўјУТФЦӨГчЈ®
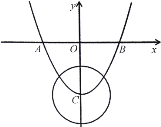
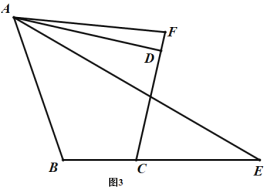
ЈЁ2Ј©ИзНј2Ј¬өг![]() ФЪ
ФЪ![]() НвЈ¬ДЗГҙ
НвЈ¬ДЗГҙ![]() Ц®јдөДКэБҝ№ШПөКЗ·сёДұдЈҝИфёДұдЈ¬ЗлЦұҪУРҙіцЛьГЗөДКэБҝ№ШПөЈ»ИфІ»ұдЈ¬ЗлЛөГчАнУЙЈ®
Ц®јдөДКэБҝ№ШПөКЗ·сёДұдЈҝИфёДұдЈ¬ЗлЦұҪУРҙіцЛьГЗөДКэБҝ№ШПөЈ»ИфІ»ұдЈ¬ЗлЛөГчАнУЙЈ®

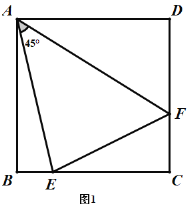
Ўҫҙр°ёЎҝЈЁ1Ј©ўЩЎчBADЈ¬ЎчCAPЈ¬ 63ЎгЈ»ўЪҰВ©ҒҰБЈҪ90ЎгЈ»ЈЁ2Ј©ёДұдЈ¬ҰБ+ҰВЈҪ90ЎгЈ®
ЎҫҪвОцЎҝ
ЈЁ1Ј©ўЩПИЦӨГчЎчBADЎХЎчCAPЈ¬ёщҫЭИ«өИИэҪЗРОөДРФЦКөГөҪCPЈҪBDЈ¬ёщҫЭөИСьИэҪЗРОөДРФЦКҪвҙрЈ»ўЪ·ВХХўЩөДЧч·ЁҪвҙрјҙҝЙЈ»
ЈЁ2Ј©№эөгAЧч![]() Ј¬ЗТADЈҪAPЈ¬Б¬ҪУDPЈ¬DBЈ¬ЦӨГчЎчBADЎХЎчCAPЈ¬ёщҫЭИ«өИИэҪЗРОөДРФЦКөГөҪPCЈҪBDЈ¬ҪбәПНјРОјЖЛгјҙҝЙЈ®
Ј¬ЗТADЈҪAPЈ¬Б¬ҪУDPЈ¬DBЈ¬ЦӨГчЎчBADЎХЎчCAPЈ¬ёщҫЭИ«өИИэҪЗРОөДРФЦКөГөҪPCЈҪBDЈ¬ҪбәПНјРОјЖЛгјҙҝЙЈ®
ҪвЈәЈЁ1Ј©ўЩЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ЎаЎПBACЈҪЎПDAPЈ¬
ЎаЎПBADЈҪЎПCAPЈ¬
ФЪЎчBADәНЎчCAPЦРЈ¬
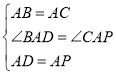 Ј¬
Ј¬
ЎаЎчBADЎХЎчCAPЈЁSASЈ©Ј¬
ЎаBDЈҪCPЈ¬ЎПBDAЈҪЎПAPCЈ¬
ЎЯ![]() Ј¬
Ј¬
ЎаBDЈҪ![]() Ј¬
Ј¬
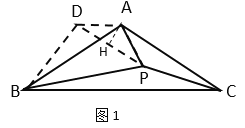
ИзНјЈ¬№эөгAЧчAHЎНDPЈ¬ҙ№ЧгОӘөгHЈ¬
ЎЯ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬
Ј¬
ЎаЎПAPDЈҪЎПADPЈҪ30ЎгЈ¬
ФЪRtЎчAPHЦРЈ¬cosЎПAPH=![]() ,
,
Ўаcos30Ўг=![]() ,
,
Ўа![]()
ЎЯ![]() Ј¬AHЎНDPЈ¬
Ј¬AHЎНDPЈ¬
ЎаDPЈҪ2PHЈҪ![]() Ј¬
Ј¬
ЎаBDЈҪDPЈ¬
ЎаЎПBPDЈҪЎПPBDЈ¬
ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]()
ЎЯ![]() Ј¬ЎПAPDЈҪ30ЎгЈ¬
Ј¬ЎПAPDЈҪ30ЎгЈ¬
ЎаЎПBPDЈҪЎПPBDЈҪ![]()
ЎаЎПBDPЈҪ![]() Ј¬
Ј¬
ЎаЎПBDAЈҪЎПBDP+ЎПADPЈҪ![]() Ј¬
Ј¬
ЎЯЎПBDAЈҪЎПAPCЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
№Кҙр°ёОӘЈәЎчBADЈ¬ЎчCAPЈ¬ 63ЎгЈ»
ўЪҰВ©ҒҰБЈҪ90ЎгЈ¬
АнУЙИзПВЈәУЙўЩөГ
ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬ЎПAPDЈҪ30ЎгЈ¬
Ј¬ЎПAPDЈҪ30ЎгЈ¬
ЎаЎПBPDЈҪЎПPBDЈҪ![]() Ј¬
Ј¬
ЎаЎПBDPЈҪ![]() Ј¬
Ј¬
ЎаЎПBDAЈҪЎПBDP+ЎПADPЈҪ![]() Ј¬
Ј¬
ЎЯЎПBDAЈҪЎПAPCЈ¬
Ўа![]() Ј¬
Ј¬
ЎаҰВ©ҒҰБЈҪ90ЎгЈ¬
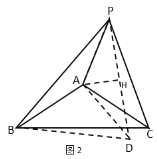
ЈЁ2Ј©ёДұдЈ¬ҰБ+ҰВЈҪ90ЎгЈ¬АнУЙИзПВЈә
№эөгAЧчЎПDAPЈҪ120ЎгЈ¬ЗТADЈҪAPЈ¬Б¬ҪУDPЈ¬DBЈ¬№эөгAЧчAHЎНDPЈ¬ҙ№ЧгОӘөгHЈ¬
ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ЎаЎПBACЈҪЎПDAPЈ¬
ЎаЎПBADЈҪЎПCAPЈ¬
ФЪЎчBADәНЎчCAPЦРЈ¬
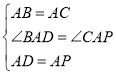 Ј¬
Ј¬
ЎаЎчBADЎХЎчCAPЈЁSASЈ©Ј¬
ЎаBDЈҪCPЈ¬ЎПBDAЈҪЎПAPCЈ¬
ЎЯ![]() Ј¬
Ј¬
ЎаBDЈҪ![]() Ј¬
Ј¬
ЎЯ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬
Ј¬
ЎаЎПAPDЈҪЎПADPЈҪ30ЎгЈ¬
ФЪRtЎчAPHЦРЈ¬cosЎПAPH=![]() ,
,
Ўаcos30Ўг=![]() ,
,
Ўа![]()
ЎЯ![]() Ј¬AHЎНDPЈ¬
Ј¬AHЎНDPЈ¬
ЎаDPЈҪ2PHЈҪ![]() Ј¬
Ј¬
ЎаBDЈҪDPЈ¬
ЎаЎПBPDЈҪЎПPBDЈ¬
ЎЯ![]() Ј¬ЎПAPDЈҪ30ЎгЈ¬
Ј¬ЎПAPDЈҪ30ЎгЈ¬
ЎаЎПBPDЈҪЎПPBDЈҪЎПAPB+ЎПAPDЈҪ![]() +30ЎгЈ¬
+30ЎгЈ¬
ЎЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ЎаЎПADBЈҪ![]() Ј¬
Ј¬
УЦЎЯЎПADPЈҪ30ЎгЈ¬
ЎаЎПBDPЈҪЎПADB+ЎПADPЈҪ![]() +30Ўг,
+30Ўг,
ЎЯЎПBPD+ЎПPBD+ЎПBDPЈҪ180Ўг,
Ўа![]() +30Ўг+
+30Ўг+![]() +30Ўг+
+30Ўг+![]() +30ЎгЈҪ180Ўг,
+30ЎгЈҪ180Ўг,
ЎаҰБ+ҰВЈҪ90ЎгЈ¬
ЎаҰБЎўҰВЦ®јдөДКэБҝ№ШПөёДұдОӘҰБ+ҰВЈҪ90ЎгЈ®