Question

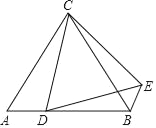
【题目】如图，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，AC=3，BC=4，则线段CD的长等于__________．

Answer 1

【答案】

【解析】

将△BCD绕点D逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图），于是得到∠CBD=∠EAD，AE=BC，根据四边形的内角和得到点C，A，E在同一条直线上，根据勾股定理即可得到结论．

解：将△BCD绕点D逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图），

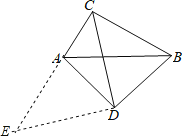
∴∠CBD=∠EAD，AE=BC，
∵∠ACB=∠ADB=90°，
∴∠CBD+∠CAD=180°，
∴∠EAD+∠CAD=180°，
∴点C，A，E在同一条直线上，且△CDE是等腰直角三角形，
∴CE=CD，
∵CE=AC+BC=7，
∴CD=（AC+BC）=，
故答案为：．