Question

【题目】已知点为平面直角坐标系中不重合的两点，以点为圆心且经过点作，则称点为的“关联点”， 为点的“关联圆”.

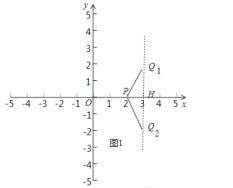
（1）已知的半径为1，在点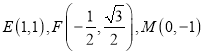中，的“关联点”为____________（填写字母）；

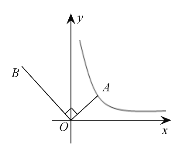
（2）若点，点，为点的“关联圆”，且的半径为，求的值；

（3）已知点，点，是点的“关联圆”，直线与轴，轴分别交于点。若线段上存在的“关联点”，求的取值范围.

Answer 1

【答案】（1）；（2）；（3）或

【解析】

（1）求出OE、OF、OM的长即可判断；
（2）如图1，过点Q作QH⊥x轴于H，利用勾股定理求解即可解决问题；
（3）求出两种特殊位置时m的值，即可得出答案.

解：（1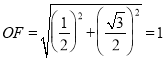）∵，，OM＝1，

∴点F、点M在⊙上，
∴F、M是⊙O的“关联点”，
故答案为：F、M；

（2）如图1，过点Q作QH⊥x轴于H．

∵PH＝1，QH＝n，PQ＝，
∴由勾股定理得，PH2＋QH2＝PQ2，即12＋n2＝()2，
解得：n＝2或2；

（3）由，知A（4，0），B（0，4）

∴AB＝，

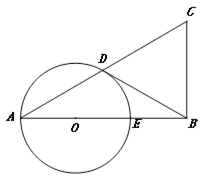
①如图2，当⊙D与AB相切于点T时，连接DT，

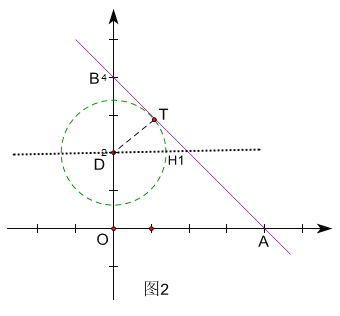
则DT⊥AB，∠DTB＝90°，

∵sin∠OBA＝sin45°＝，即，

∴DT＝DH1＝，

∴m1＝；

②如图3，当⊙D过点A时，连接AD，

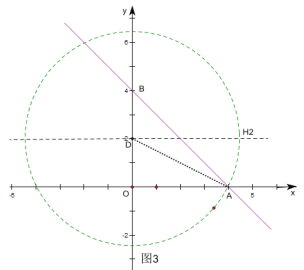
由勾股定理得DA＝，

∴DA＝DH2＝，

综合①②可得：的取值范围为或．